[Toán 7] Bàn luận : Từ một bài toán hình đơn giản.

H

harrypham

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

TỪ MỘT BÀI TOÁN HÌNH ĐƠN GIẢN​

Thông qua chương trình học lớp 7, dường như tồn tại rất nhiều bài toán hay và khó. Tuy nhiên mình cũng nhận thấy hầu hết các bài toán về chứng minh tam giác bằng nhau đều quy về một bài toán, có thể coi nó là bài toán dễ.

Bài toán gốc. Cho hai đường thẳng [TEX]AB[/TEX] và [TEX]CD[/TEX] cắt nhau (tại O) tại trung điểm mỗi đường. Chứng minh [TEX]\bigtriangleup OAC= \bigtriangleup OBD[/TEX].

Lời giải.
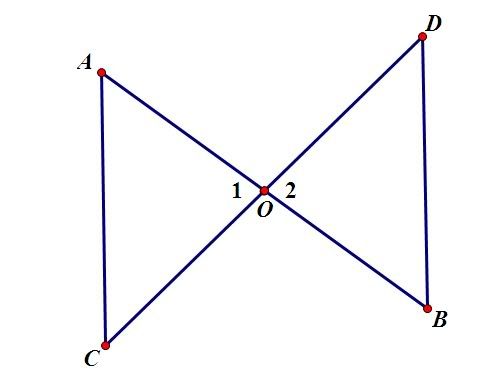
untitled-11.jpg
Xét [TEX]\bigtriangleup OAC[/TEX] và [TEX]\bigtriangleup OBD[/TEX] có
+ [TEX]AO=BO[/TEX] (gt)
+ [TEX]CO=DO[/TEX] (gt)
+ [TEX]\widehat{O_1}= \widehat{O_2}[/TEX] (đối đỉnh)

[TEX]\Rightarrow \bigtriangleup OAC= \bigtriangleup OBD[/TEX] (c.g.c)

Bây giờ, hãy thử nghĩ xem, ta đã chứng minh được [TEX]\bigtriangleup OAC= \bigtriangleup OBD[/TEX], như vậy thì [TEX]AC=BD[/TEX] và [TEX]\widehat{CAB}= \widehat{ABD}[/TEX], cũng từ [TEX]\widehat{CAB}= \widehat{ABD}[/TEX] thì dẫn tới [TEX]AC // BD[/TEX]. Tương tự dễ dàng chứng minh được [TEX]AD=BC[/TEX] và [TEX]AC//BD[/TEX]. Ta rút ra bài toán mới sau:

Bài toán 1. Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm mỗi đường (tại O). Chứng minh
a) [TEX]AC=BD[/TEX] và [TEX]AC//BD[/TEX].
b) [TEX]AD=BC[/TEX] và [TEX]AD//BC[/TEX].

Hãy cùng mở rộng tiếp nào.

 
H

harrypham

Ta có thể mở rộng bài toán với ba đường thẳng cắt nhau tại trung điểm mỗi đường như sau:

Bài toán 2. Cho ba đoạn thẳng [TEX]AM,CK,BN[/TEX] cắt nhau tại trung điểm [TEX]O[/TEX] mỗi đường. Chứng minh tam giác [TEX]ABC[/TEX] bằng tam giác [TEX]MNK[/TEX].
Hãy thử sức với bài này.
 
M

minhtuyb

Áp dụng kết quả của bài toán gốc, ta lần lượt có:
[TEX]\Delta AOC=\Delta MOK(c.g.c)\Rightarrow AC=MK(1)[/TEX]
[TEX]\Delta COB=\Delta KON(c.g.c)\Rightarrow BC=NK(2)[/TEX]
[TEX]\Delta AOb=\Delta MON(c.g.c)\Rightarrow AB=MN(3)[/TEX]
-Từ (1),(2) và (3) [TEX]\Rightarrow \Delta ABC=\Delta MNK(c.c.c)[/TEX]
 
H

harrypham

Một số bài toán trong sách bài tập toán 7 cũng là dạng của bài toán gốc.

Bài toán 3. Cho tam giác ABC, D trung điểm AB. Đường thẳng qua D và song song với BC cắt AC ở E. Đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh:
a) [TEX]AD=EF[/TEX]
b) [TEX]\bigtriangleup ADE= \bigtriangleup EFC[/TEX]
c) [TEX]AE=EC[/TEX]

Bài toán 4. Cho tam giác ABC, D trung điểm AB. E trung điểm AC. Vẽ F sao cho E là trung điểm DF. Chứng minh rằng:
a) [TEX]DB=CF[/TEX].
b) [TEX]\bigtriangleup BDC= \bigtriangleup FCD[/TEX].
c) [TEX]DE//BC[/TEX] và [TEX]DE= \frac{1}{2}BC[/TEX].
 
B

braga

Mình xin chém bài 3 trước !



a, Xét [TEX]\Delta BDF[/TEX] và [TEX]\Delta EFD[/TEX] có:

[TEX]\hat{F_2}=\hat{D_1}(BD//EF) \\\ DF \ chung \\\ \hat{F_3}=\hat{D_2}(BD//EF) \\\ \Rightarrow \Delta BDF=\Delta EFD(g.c.g) \Rightarrow EF=BD[/TEX]

Mà [TEX]BD=AD \Rightarrow EF=AD(dpcm)[/TEX]

b, Ta có: [TEX]\hat{E_1}=\hat{E_2}(dd) \ ma \ \hat{E_2}=\hat{A} ( EF//AB) \Rightarrow\hat{A}=\hat{E_1} [/TEX]

[TEX]\hat{D_1}+\hat{D_2}+\hat{D_3}=\hat{F_1}+\hat{F_2}+\hat{F_3}=180^o \\\ ma \ \hat{D_1}+\hat{D_2}=\hat{F_2}+\hat{F_3} \Rightarrow \hat{D_3}+\hat{F_1}[/TEX]

Xét [TEX]\Delta ADE[/TEX] và [TEX]\Delta EFC[/TEX] có:

[TEX]\hat{E_1}=\hat{A}[/TEX] ( CM trên)

[TEX]EF=AD(gt)[/TEX]

[TEX]\hat{D_3}+\hat{F_1}[/TEX] ( CM trên)

[TEX]\Rightarrow \Delta ADE=\Delta EFC(g.c.g)[/TEX]

c, Từ [TEX] \Delta ADE=\Delta EFC \Rightarrow AE=EC[/TEX] ( 2 cạnh tương ứng)
 
B

braga

Bài 4:



a, Xét [TEX]\Delta ADE[/TEX] và [TEX]\Delta CFE[/TEX] có:

[TEX]DE=FE(gt) \\\ \hat{E_1}=\hat{E_2}(dd) \\\ AE=CE(gt) \\\ \Rightarrow \Delta ADE=\Delta CFE(c.g.c) \\\ \Rightarrow AD=CF \ ma \ BD=AD \Rightarrow BD=CF(dpcm) \Rightarrow \hat{C_2}=\hat{A} \Rightarrow AB//CF[/TEX]

b, Xét [TEX]\Delta BDC[/TEX] và [TEX]\Delta FCD[/TEX] có:

[TEX]CF=BD \\\ \hat{D_1}=\hat{FCD}(AB//CF) \\\ DC \ chung \\\ \Rightarrow \Delta BDC=\Delta FCD(c.g.c)[/TEX]

c, [TEX]\Delta BDC=\Delta FCD \Rightarrow \{\hat{D_2}=\hat{C_1} \Rightarrow DE//BC \\ DF=BC \ ma \ DE=\frac{1}{2}DF \Rightarrow DE=\frac{1}{2}BC[/TEX]

 
H

harrypham

Bài toán 5. Cho tam giác ABC. Vẽ đường thẳng xy qua A song song BC. Lấy M trên BC, vẽ các đường thẳng đi qua M song song AB,AC lần lượt cắt xy tại D,E. Chứng minh
a) Tam giác ABC bằng tam giác MDE.
b) Ba đường thẳng AM,BD,CE đồng quy.

Bây giờ bạn đã nắm rõ mục đích topic, liệu bạn có thể tự biên chế ra một bài toán mới dựa trên cơ sở bài toán gốc không ?
 
K

kieuphuong232

Cho tam giác ABC có các góc đều nhọn, và AB < AC. Phân giác của góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F.
a) Chứng minh AB = AF.
b) Qua F vẽ đường thẳng song song với BC, cắt AE tại H. Lấy điểm K nằm giữa D và C sao cho FH = DK. Chứng minh DH = KF và DH // KF.
c) Chứng minh góc ABC lớn hơn góc C.
 
H

harrypham

kieuphuong232 said:
Cho tam giác ABC có các góc đều nhọn, và AB < AC. Phân giác của góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F.
a) Chứng minh AB = AF.
b) Qua F vẽ đường thẳng song song với BC, cắt AE tại H. Lấy điểm K nằm giữa D và C sao cho FH = DK. Chứng minh DH = KF và DH // KF.
c) Chứng minh góc ABC lớn hơn góc C.
Bấm để xem đầy đủ nội dung ...
untitled-61.jpg


a) Ta chứng minh $\triangle AEB = \triangle AEF$ (g.c.g) (do chung $AE, \; \widehat{BAE}= \widehat{FAE}, \; \widehat{AEB}= \widehat{AEF}=90^o$).
nên $AB=AF$.

b) Nối $D$ với $F$. Ta có $\triangle DFH= \triangle FDK$ (c.g.c) (chugn $DF, \; \widehat{HFD}= \widehat{FDK}, \; HF=DK$ )
nên $HD=FK$ và $\widehat{DFK}= \widehat{FDH}$ suy ra $HD//FK$.

c) Do $AB<AC$ nên $\widehat{B}> \widehat{C}$.
​
 
T

taitutungtien

Cho tam giác ABC có các góc đều nhọn, và AB < AC. Phân giác của góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F.
a) Chứng minh AB = AF.
b) Qua F vẽ đường thẳng song song với BC, cắt AE tại H. Lấy điểm K nằm giữa D và C sao cho FH = DK. Chứng minh DH = KF và DH // KF.
c) Chứng minh góc ABC lớn hơn góc C.
 
T

taitutungtien

Cho tam giác ABC có các góc đều nhọn, và AB < AC. Phân giác của góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F.
a) Chứng minh AB = AF.
b) Qua F vẽ đường thẳng song song với BC, cắt AE tại H. Lấy điểm K nằm giữa D và C sao cho FH = DK. Chứng minh DH = KF và DH // KF.
c) Chứng minh góc ABC lớn hơn góc C.


a,xét tam giac AEB và tam giác AEFcó:
\{AEB}
 
You must log in or register to reply here.
Top Bottom