Toán [Toán 7] Bài tập Hình

[ghgh2323]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho góc xOy nhọn. A thuộc tia Ox, B thuộc tia Oy, sao cho OA=OB. Từ A kẻ đg thẳng vuông góc với tia Ox cắt Oy ở E. Từ B kẻ đg thẳng vuông góc với Oy cắt Ox ở F. AE cắt BF tại I
a. AE = BF
b. tam giác AFI = tam giác BEI
c. OI là tia phân giác của góc AOB

 

[realme427]

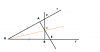
Cho góc xOy nhọn. A thuộc tia Ox, B thuộc tia Oy, sao cho OA=OB. Từ A kẻ đg thẳng vuông góc với tia Ox cắt Oy ở E. Từ B kẻ đg thẳng vuông góc với Oy cắt Ox ở F. AE cắt BF tại I
a. AE = BF
b. tam giác AFI = tam giác BEI
c. OI là tia phân giác của góc AOB

a,-Xét:[tex]\Delta OEA\left ( \widehat{A}=90^{\circ} \right ) và \Delta OBF\left ( \widehat{B}=90^{\circ} \right ) có:[/tex]
+[tex]\widehat{O}[/tex] là góc chung
+[tex]OA=OB\left ( gt \right )[/tex]
-Vậy: [tex]\Delta OEA=\Delta OBF\left ( cgv-gn \right )[/tex]
c, -Ta có: +OF=OA+AF
+OE=OB+BE
-MÀ: +[tex]OA=OB\left ( gt \right )[/tex]
+[tex]BE=AF\left ( cmt \right )[/tex]
[tex]\Rightarrow OF=OE[/tex]
-XÉt: [tex]\Delta EIO và \Delta FIO có:[/tex]
+[tex]\widehat{F}=\widehat{E}\left ( 2 góc tương ứng \right )[/tex]
+[tex]IE=IF\left ( 2 cạnh tương ứng \right )[/tex]
+OF=OE[tex]\left ( cmt \right )[/tex]
-Vậy....
b, -Suy ra: [tex]OE=OF\left (2 cạnh tương ứng \right )[/tex]
-Ta có: +[tex]OE=OB+BE[/tex]
+[tex]OF=OA+AF[/tex]
-MÀ: [tex]OA=OB và b, -Suy ra: [tex]OE=OF\left (2 cạnh tương ứng \right )[/tex]
-Ta có: +[tex]OE=OB+BE[/tex]
+[tex]O=OA+AF[/tex]
-MÀ: [tex]OA=OB và OF=OE(cmt)\Rightarrow BE=AF[/tex]
-Bạn tự c/m tam giác AFI và BEI nhé theo trường hợp: cgnv-gn

 

[mikhue]

Cho góc xOy nhọn. A thuộc tia Ox, B thuộc tia Oy, sao cho OA=OB. Từ A kẻ đg thẳng vuông góc với tia Ox cắt Oy ở E. Từ B kẻ đg thẳng vuông góc với Oy cắt Ox ở F. AE cắt BF tại I
a. AE = BF
b. tam giác AFI = tam giác BEI
c. OI là tia phân giác của góc AOB

a, xét tam giác AOE và tam giác BOF ta có:
góc xOy là góc chung
AO = BO
=> tam giác AOE = tam giác BOF (cạnh huyền góc nhọn)
=> AE = BF (2 cạnh tương ứng)
=> OE = OF (2 cạnh tương ứng)
b, ta có OE = OF (cm trên)
mà OE + EB = OB
OF + FA = OA
OA = OB
=> FA = EB
* Xét tam giác AFI và tam giác BEI có:
góc AIF = góc BIE ( 2 góc đối đỉnh)
FA = EB( cm trên)
=> tam giác AFI = tam giác BEI

 

[mikhue]

View attachment 36254

a, xét tam giác AOE và tam giác BOF ta có:
góc xOy là góc chung
AO = BO
=> tam giác AOE = tam giác BOF (cạnh huyền góc nhọn)
=> AE = BF (2 cạnh tương ứng)
=> OE = OF (2 cạnh tương ứng)
b, ta có OE = OF (cm trên)
mà OE + EB = OB
OF + FA = OA
OA = OB
=> FA = EB
* Xét tam giác AFI và tam giác BEI có:
góc AIF = góc BIE ( 2 góc đối đỉnh)
FA = EB( cm trên)
=> tam giác AFI = tam giác BEI

bạn ơi sao lấy bài mình vậy?

 

[bạchlinh0912]

hình nè