[Toán 7]Bài hình

[huonggiang22]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho tam giác ABC, góc A bằng 60 do^ , phân giác BM và CN cắt nhau tại O(M,N thuộc AC,AB). Chứng minh:
a) OM = ON
b) Có nhận xét gì về các góc của tgiác OMN?

 

[computerscience]

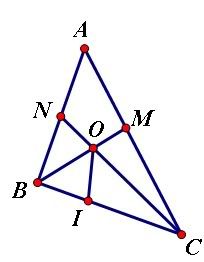
Vì [tex] \hat{A} =60^o[/tex] nên :
[tex]\widehat{ABC}+\widehat{ACB}=120^o[/tex]
Mà BM là phân giác của [tex]\widehat{ABC}[/tex] nên :
[tex]\widehat{OBC}=\frac{1}{2}.\widehat{ABC}[/tex]
Chứng minh tương tự ta cũng có:
[tex]\widehat{OCB}=\frac{1}{2}.\widehat{ACB}[/tex]
[tex]\Rightarrow\widehat{OBC}+\widehat{OCB}=\frac{1}{2}(\widehat{ABC}+\widehat{ACB})[/tex]
[tex]\Rightarrow\widehat{OBC}+\widehat{OCB}=60^{o}[/tex]
[tex]\Leftrightarrow \widehat{BOC}=120^{o}[/tex]
[tex]\Rightarrow\widehat{NOB}=\widehat{MOC}=60^{o}[/tex] ( Cùng kề bù với [tex]\widehat{BOC}[/tex])
Vẽ tia phân giác OI của [tex]\widehat{BOC}[/tex]
[tex]\Rightarrow\widehat{IOB}=\widehat{IOC}=60^{o}[/tex]
Ta có tam giác IOC bằng tam giác MOC (g-c-g) nên
[tex]\Rightarrow OI=OM (1) [/tex]
Chứng minh tương tự ta cũng có
[tex]OI=ON (2) [/tex]
Từ [tex](1)[/tex] và [tex](2)[/tex] ta suy ra :
[tex]OM=ON (dpcm)[/tex]

 

[ngobin3]

Toán 7

Có một bài tương tự như vậy tại đây:
Đề là thế này (tương tự nhau)
Cho [TEX]\triangle{MNQ}[/TEX] có [TEX]\hat{Q}[/TEX] = [TEX]60^0[/TEX], tia phân giác ME ([TEX]E \in NQ[/TEX]) của [TEX]\triangle{MNQ}[/TEX] cắt tia phân giác NK ([TEX]K \in MQ[/TEX]) của [TEX]\triangle{QNM}[/TEX] tại điểm H. Chứng minh [TEX]HK = HE[/TEX]
Đây là cách giải của thuhien

Từ H kẻ tia phân giác [TEX]\widehat{MHN}[/TEX] cắt MN tại I.
Tam giác MQN có [TEX]\widehat{MQN}+\widehat{QMN}+\widehat{QNM}=180^o[/TEX]. \Rightarrow[TEX] \widehat{QMN}+\widehat{QNM}=120^o[/TEX] \Rightarrow [TEX] \frac{\widehat{QMN}}{2}+\frac{\widehat{QNM}}{2}= 60^o[/TEX]. Hay: [TEX]\widehat{HMN}+\widehat{HNM}=60^o[/TEX]. Mà: [TEX]\widehat{HMN}+\widehat{HNM}+\widehat{MHN}=180^o[/TEX](3 góc trong tam giác) \Rightarrow [TEX] \widehat{MHN}=120^o[/TEX] \Rightarrow [TEX]\widehat{MHI}=\widehat{IHN}=60^o[/TEX] (MI là phân giác [TEX]\widehat{MHN}[/TEX])
\Rightarrow [TEX]\widehat{MHK}=60^o[/TEX]. (Kề bù với [TEX]\widehat{MHN}[/TEX])
+[TEX]\widehat{MHK}=\widehat{EHN}=60^o[/TEX]

* Xét tam giác MHI và tam giác MHK ta có:
+ [TEX]\widehat{KMH}=\widehat{HMI}[/TEX] (MH là phân giác [TEX]\widehat{QMN}[/TEX])
+ MH chung
+ [TEX]\widehat{KHM}=\widehat{MHI}=60^o[/TEX]
\Rightarrow tam giác MHI và tam giác MHK (g.c.g)
\Rightarrow HI=HK (2 cạnh tg ứng) (1)

* Xét tam giác IHN và tam giác EHN ta có:
+ [TEX]\widehat{INH}=\widehat{HNE}[/TEX] (NH là phân giác [TEX]\widehat{QNM}[/TEX])
+ NH chung
+ [TEX]\widehat{IHN}=\widehat{EHN}=60^o[/TEX]
\Rightarrow tam giác IHN và tam giác EHN (g.c.g)
\Rightarrow HI=HE (2 cạnh tg ứng) (2)

* Từ (1) và (2) \Rightarrow đpcm

Cách này hơi dài, bạn nào có cách ngắn hơn hem

 

[thienthan04091999]

Ke OI la tia phan giac goc BOC( I thuoc BC)
Ta co: goc NOC= goc BOC+ goc BON \Rightarrowgoc BON=180 độ - goc BOC =60độ
goc BOM= goc BOC + goc COM\Rightarrowgoc COM= 180độ -goc BOC=60độ
tam giac BON=tam giac BOI(g-c-g)\RightarrowON=OI(1)
tam giac OCI= tam giac OCM(g-c-g)\RightarrowOI=OM(2)
Từ (1)và (2)\RightarrowOM=ON(cùng =OI)