Toán [Toán 12] Tính khoảng cách giữa SD và AC

[Starter2k]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

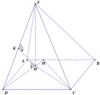
Cho hình chóp S. ABCD có đáy là hình chữ nhật. AB = 2a; AD = a. Trên cạnh AB lấy điểm M sao cho [tex]AM = \frac{a}{2}[/tex] H là giao điểm của AC và MD. Biết SH vuông góc với mặt phẳng (ABCD) và SH=a. Tính khoảng cách giữa hai đường thẳng SD và AC theo a.
A. [tex]\frac{a}{3}[/tex]
B. [tex]\frac{2a}{3}[/tex]
C. $a$
D. $2a$
@dragonsquaddd @thangnguyenst95 Mọi người giúp em với ạ ^^

 

[dragonsquaddd]

ta có: từ dữ kiện đề ra ta được AC vuông góc DM

Xét tam giác SHD vuông tại H thì ta được khoảng cách từ SD đến AC chính là đoạn thẳng HI với HI vuông góc với SD

 

[Starter2k]

ta có: từ dữ kiện đề ra ta được AC vuông góc DM

Xét tam giác SHD vuông tại H thì ta được khoảng cách từ SD đến AC chính là đoạn thẳng HI với HI vuông góc với SD

Thực ra e đã xác định được đoạn nào là khoảng cách. Nhưng mà em ko biết định lượng như thế nào để ra được kết quả .....

E gọi độ dài đoạn là HK ạ. Em ko tính được HD. Anh giúp em với

 

[dragonsquaddd]

hệ thức lượng trong tam giác vuông ADC: [tex]\frac{1}{HD^2}=\frac{1}{AD^2}+\frac{1}{AC^2}[/tex]

 

[Starter2k]

hệ thức lượng trong tam giác vuông ADC: [tex]\frac{1}{HD^2}=\frac{1}{AD^2}+\frac{1}{AC^2}[/tex]

Đúng rồi. Tự nhiên em quên mất hệ thức này ... @_@ E cảm ơn anh ạ.

Nhân tiện anh giúp em cái bài toán thực tế này với ạ ^^

 

[dragonsquaddd]

@huuthuyenrop2 chú xem qua bài này coi :v nhân tiện cho anh hỏi công thức lãi kép là gì ấy nhỉ

 

[dragonsquaddd]

bài toán dạng này em có thể làm mò bằng cách bấm máy tính thử từng đáp án nhé

 

[thangnguyenst95]

Trước tiên ta chứng minh

: $\begin{align}

& AC\bot MD. \\

& A\vec{C}.M\vec{D}=(A\vec{D}+D\vec{C}).(M\vec{A}+A\vec{D})=D\vec{C}.M\vec{A}+A\vec{D}.A\vec{D} \\

& \\

\end{align}$

$=-\frac{a}{2}.2a+a.a=0$ .

$\begin{align}

& AC\bot AH,AC\bot MD \\

& \Rightarrow AC\bot (AMD) \\

& \\

\end{align}$

Trong $(AMD)$ kẻ HI $\bot $ SD (I thuộc SD).

Vì $AC\bot (AMD)\Rightarrow AC\bot HI$

Vậy HI là đường vuông góc chung của AC và SD.

Xét tam giác SHD vuông tại H,

\[\begin{align}

& \frac{1}{H{{I}^{2}}}=\frac{1}{S{{H}^{2}}}+\frac{1}{H{{D}^{2}}}=\frac{1}{a{}^{2}}+\frac{1}{{{a}^{2}}}=\frac{2}{{{a}^{2}}}. \\

& \Rightarrow HI=a/\sqrt{2} \\

\end{align}\]