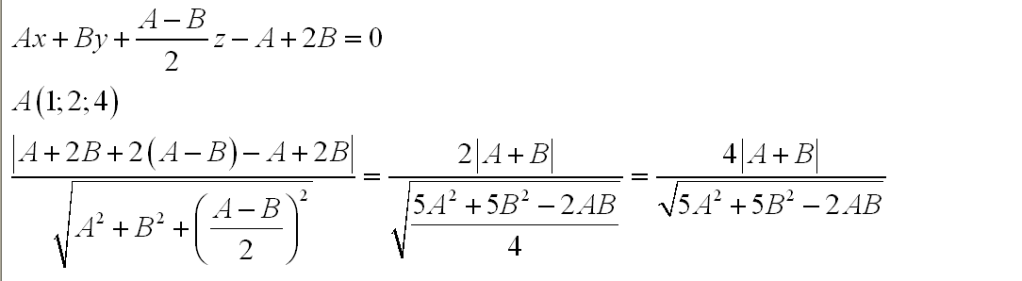D
duy_vip
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
trog ko jan Oxyz cho điểm A(1,2,4) và đường thẳng (d) [TEX]\frac{x-1}{-1}[/TEX] = [TEX]\frac{y+2}{1}[/TEX] = [TEX]\frac{z}{2}[/TEX]
viết pt mq (P) chứa (d) sao cho khoảng cách từ A tới (P) lớn nhất


viết pt mq (P) chứa (d) sao cho khoảng cách từ A tới (P) lớn nhất