[toán 11]phép biến hình-đối xứng tâm

[happylife71]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

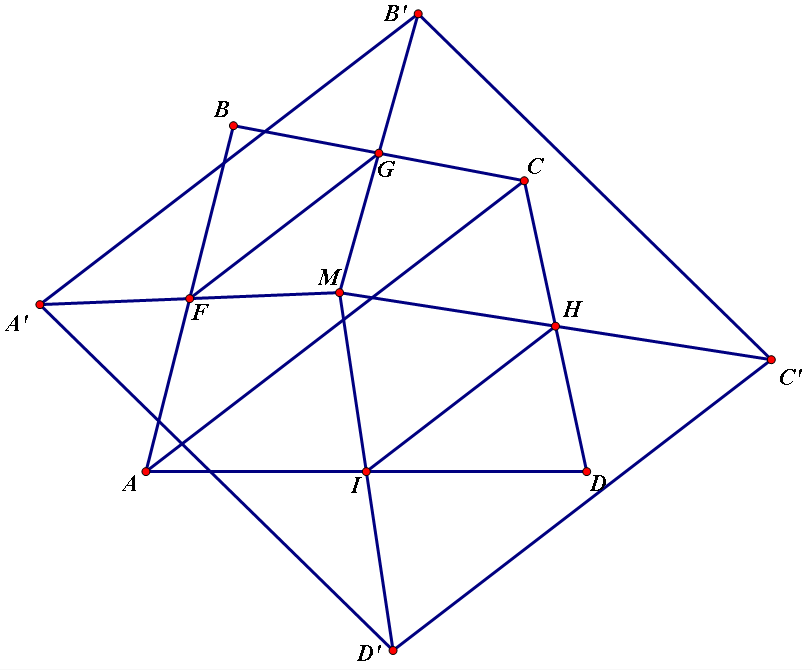
Câu 1:Điểm M thuộc miền trong của tứ giác lồi ABCD.Gọi A',B',C',D' lần lượt là điểm đối xứng của M qua trung điểm các cạnh AB,BC,CD,DA.chứng minh tứ giác A'B'C'D' là hình bình hành

Câu 2:Một đường thẳng đi qua tâm O của hình bình hành ABCD cắt các cạnh DC,AB tại P và Q.Chứng minh rằng các giao điểm của các đường thẳng AP,BP,CQ,DQ với các đường chéo của hình bình hành là các đỉnh của 1 hình bình hành mới

 

[demon311]

Ta có:

FG là đường trung bình trong tam giác BAC nên $FG // AC$ và $FG=\dfrac{1}{2}AC$

FG là đường trung bình trong tam giác MA'B' nên $FG // A'B'$ và $FG=\dfrac{1}{2}A'B'$

Do đó $AC=A'B'$ và $AC //A'B'$

Tương tự với IH

Nên $C'D'=AC$ và $C'D' // AC$

TỪ đó suy ra điều cần chứng minh

Bài này lớp 8 làm cũng được mà