[Toán 11] Hình học không gian

D

debay

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Các bạn giúp mình gấp bài 18 trang 103 SGK Hình học 11 với ạ. Đề bài như sau:

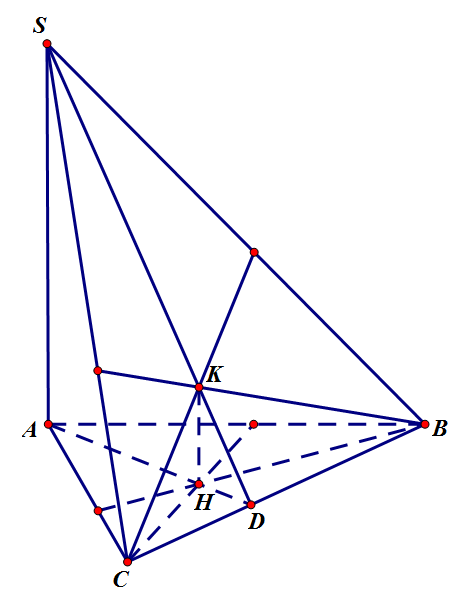
Cho hình chóp S.ABC có SA vuông với mp (ABC), các tam giác ABC và SBC không vuông. Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Chứng minh rằng:
a) AH, SK, BC đồng quy;
b) SC vuông góc với mp (BHK);
c) HK vuông góc với mp (SBC).

Cảm ơn các bạn rất nhiều!
 
N

nice_vk

Cho mình hỏi chương toán 11 hình của bạn là chương mấy, tên gì. có thể mình tìm được.
 
D

demon311

Untitled_zpswd0tmqf6.png


Gọi D là giao điểm của Ah và BC

Ta cần chứng minh $SD \perp BC$

Thật vậy, ta có:

$BC \perp AD \\
BC \perp SA \\
SA,AD \subset (SAD) \\
\Rightarrow BC \perp (SAD) \Rightarrow BC \perp SD$

Mà $SK \perp BC$ nên $D \in SK$, hay $SK,AH,BC$ đồng quy tại K

b) Ta có:

$BH \perp AC \\
BH \perp SA \\
\Rightarrow BH \perp SC$

Lại có $SC \perp BK \Rightarrow SC \perp (BHK)$

c) $HK \perp BC$ (suy ra từ câu b)

$HK \perp BC$ (do $BC \perp (SAD)$)

Do đó $HK \perp (SBC)$

Xong

Bấm thank phát
 
  • Like
Reactions: Tên tui nè and huele2000
You must log in or register to reply here.
Top Bottom