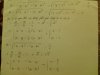Bài 1. Trong mpOxy cho tam giác ABC với A(–2;3) B(1/4; 0) và C(2;0)
Tìm tâm J đường tròn nội tiếp tam giác ABC.
Mình làm chưa chắc đúng đoạn cuối nhưng bạn cứ xem nhé
Gọi J(a;b)
Vì J là tâm đường tròn nội tiếp tam giác ABC
=> Cả đường tròn nằm trong tam giác => tâm nằm trong tam giác
BC là cạnh đáy => [tex]\Leftrightarrow x_{B}\leq x_{J}\leq x_{C}[/tex]
Bạn lập phương trình đường thẳng của 3 cạnh tam giác được
pt AB (d1) : 4x+3y-1=0
pt AC (d2): 3x+4y-6=0
pt BC (d3) : x+0y=0 (chính là trục Ox)
Bạn tìm độ dài từ I đến 3 cạnh của tam giác (tức là độ dài từ I đến 3 đường thẳng trên)
[tex]d_{(J;d1)}=\frac{\left | 4a+3b-1 \right |}{\sqrt{4^{2}+3^{2}}}=\frac{\left | 4a+3b-1 \right |}{5}[/tex]
[tex]d_{(J;d2)}=\frac{\left | 3a+4b-6 \right |}{\sqrt{3^{2}+4^{2}}}=\frac{\left | 3a+4b-1 \right |}{5}[/tex]
[tex]d_{(J;d3)}=\frac{\left | a+0.b \right |}{\sqrt{1^{2}+0^{2}}}=\left | a \right |[/tex]
Vì J là tâm đường tròn nội tiếp tam giác ABC
=> [tex]d_{(I;d1)}=d_{(I;d2)}[/tex]
[tex]\Leftrightarrow \frac{\left | 4a+3b-1 \right |}{5}=\frac{\left | 3a+4b-1 \right |}{5}[/tex]
[tex]\Leftrightarrow \left | 4a+3b-1 \right |=\left | 3a+4b-1 \right |[/tex]
[tex]\Leftrightarrow (4a+3b-1)^{2}=(3a+4b-1)^{2}[/tex]
Dùng hằng đẳng thức thứ 3 đưa về phương trình tích
[tex]\Leftrightarrow (a+b-1)(a-b+5)=0[/tex]
+) a+b-1=0 => b=1-a => I(a;1-a)
[tex]d_{(I;d1)}=d_{(I;d3)}[/tex]
[tex]\Leftrightarrow \frac{\left | 4a+3b-1 \right |}{5}=\left | a \right |[/tex]
Thế b=1-a vào và giải phương trình bằng cách bình phương tìm được a=1/2 hoặc a=-1/3
_ Với a=1/2 => J(1/2;1/2) (thỏa mãn điều kiện ban đầu)
_ Với a=-1/3 => J(-1/3;4/3) (thỏa mãn điều kiện ban đầu)
Làm tương tự với trường hợp a-b+5=0 nhé
Kết quả cuối cùng : Điểm J(1/2;1/2) (muốn kiểm chứng bạn dùng vở ô ly vẽ ra là thấy đúng :v )
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
