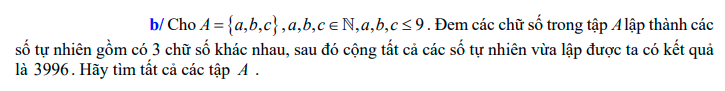Không mất tính tổng quát, giả sử [imath]a<b<c[/imath]. Xét các trường hợp.
+ [imath]a \neq 0[/imath]. Nhận thấy ta có thể lập được [imath]3!=6[/imath] số. Trong [imath]6[/imath] số đó, số lần xuất hiện của mỗi chữ số [imath]a,b,c[/imath] tại các hàng trăm, chục, đơn vị là như nhau do vai trò [imath]3[/imath] số như nhau và bằng 2. Cho nên tổng các số lập được cũng bằng [imath]2(a+b+c)(1+10+100)=3996[/imath]
Từ đó [imath]a+b+c=18[/imath].
+ [imath]a=0[/imath]. Tương tự thì nếu ta xét tổng số hoán vị [imath]3[/imath] số đó thì sẽ có [imath]2[/imath] số không thỏa mãn là [imath]\overline{0bc}, \overline{0cb}[/imath]
Từ đó tổng các số lập được bằng [imath]2(b+c)(1+10+100)-11(b+c)=3996[/imath]. Dễ thấy không thỏa mãn.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
Tổ hợp xác suất
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
