View attachment 135091
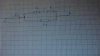
[tex]U_{AB}=24V, R_{1}=3\Omega, R_{2}=5\Omega, R_{3}=2\Omega, R_{4}=2,4\Omega[/tex]
a) Tính U, I qua các điện trở.
b) Tính A, P trong [tex]3\tfrac{1}{2}[/tex]h trong toàn mạch.
c) Mắc vào hai điểm A, D một ampe kế R[tex]_{A}[/tex] [tex]\approx[/tex]0. Tìm số chỉ A.
d) tháo bỏ A thay đổi [tex]R_{2}[/tex]. Tính [tex]R_{2}[/tex] để công suất tỏa nhiệt qua [tex]R_{2}[/tex] cực đại. Tính [tex]P_{R2 max}[/tex].
e) cần phải ghép vào [tex]R_{2}[/tex] điên trở [tex]R_{x}[/tex] thế nào để công suất tỏa nhiệt qua [tex]R_{2x}[/tex] lớn nhất. Nêu cách ghép [tex]R_{x}[/tex] và tính công suất đó.
Nếu em nhìn không lầm thì mạch là: [TEX]R_4[/TEX] nt ([TEX]R_3[/TEX] // ([TEX]R_1[/TEX] nt [TEX]R_2[/TEX]))
a,
[tex]R_{td}=R_4+\frac{(R_1+R_2).R_3}{R_1+R_2+R_3}=4\ (\Omega )[/tex]
=> [tex]I_4=I_m=\frac{U_{AB}}{R_{td}}=\frac{24}{4}=6 \ (A)[/tex]
=> [tex]U_4=I_4.R_4=6.2,4=14,4 \ (V)[/tex]
=> [tex]U_3=U_{12}=U_{AB}-U_4=24-14,4=9,6 \ (V)[/tex]
=> [tex]I_3=\frac{U_3}{R_3}=\frac{9,6}{2}=4,8 \ (A)[/tex]
=> [tex]I_1=I_2=\frac{U_{12}}{R_1+R_2}=\frac{9,6}{8}=1,2 \ (A)[/tex]
=> [tex]\left\{\begin{matrix} U_1=I_1.R_1=1,2.3=3,6 \ (V) \\ U_2=I_2.R_2=1,2.5=6 \ (V) \end{matrix}\right.[/tex]\
b, Tự làm được không ạ?
c,
Mắc Ampe kế có [tex]R_A\approx 0[/tex] vào hai điểm A và D
=> Chập A với D
Mạch điện tương đương: [TEX]R_2[/TEX] // ([TEX]R_3[/TEX] nt ([TEX]R_1[/TEX] // [TEX]R_4[/TEX]))
Ta có: [tex]I_A=I_2-I_1[/tex] (1)
Tính như câu a,
[tex]R_{td}=\frac{R_2.(R_3+\frac{R_1.R_4}{R_1+R_4})}{R_2+R_3+\frac{R_1.R_4}{R_1+R_4}}=...[/tex]
=> [tex]I_m=\frac{U_{AB}}{R_{td}}=...[/tex]
=> [tex]I_2=\frac{U_2}{R_2}=\frac{U_{AB}}{R_2}=...[/tex]
=> [tex]I_3=I_{14}=I_m-I_2=...[/tex]
=> [tex]U_3=I_3.R_3=...[/tex]
=> [tex]U_1=U_4=U_{AB}-U_3=...[/tex]
=> [tex]I_1=\frac{U_1}{R_1}=...[/tex]
Thay [tex]I_1[/tex] và [tex]I_2[/tex] vừa tính được vào (1) sẽ tính được [TEX]I_A[/TEX]
d,
Sau khi tháo bỏ [TEX]R_2[/TEX] thì mạch sẽ trở lại như mạch câu a: [TEX]R_4[/TEX] nt ([TEX]R_3[/TEX] // ([TEX]R_1[/TEX] nt [TEX]R_2[/TEX]))
Ta có công thức: [tex]P_2=I_2^2.R_2[/tex] (2)
Lại phải tính lại từ đầu :<
Tính theo các bước như ở câu a
Sẽ được [tex]I_2[/tex] và [tex]R_2[/tex] (sẽ có ẩn [tex]R_2[/tex])
Thay [tex]I_2[/tex] và [tex]R_2[/tex] vừa tính được vào công thức (2)
Sau đó dùng BĐT Cauchy để tìm max
Câu b, e em lười quá :<
Anh/Chị cố gắng tự làm nha ~~
Có gì thắc mắc cứ hỏi em ạ ^^
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
