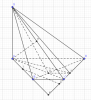
Cho hình chóp S.ABCD có [tex]SA\perp (ABCD)[/tex] . ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD với [tex]AD=2a[/tex]. I là trung điểm AB. Khoảng cách từ I đến mp (SCD) là [tex]\frac{3a\sqrt{3}}{8}[/tex]. Gọi O là giao điểm của AC và BD. Tính:
a, Thể tích S.ABCD
b, Góc giữa SO và AD
a) Do $ABCD$ là nửa lục giác nên $AB=BC=CD=\dfrac{AD}{2}=a$
$C$ thuộc đường tròn đường kính $AD\Rightarrow \widehat{ACD}=90^\circ$
Mà $CD\bot SA$
Suy ra $CD\bot(SAC)$
Kẻ $AH\bot SC$
$CD\bot(SAC)\Rightarrow AH\bot CD$
Suy ra $AH\bot(SCD)\Rightarrow d(A,(SCD))=AH$
Gọi $K$ là giao điểm của $AB$ và $CD$
$BC//AD\Rightarrow \dfrac{BC}{AD}=\dfrac{BK}{AK}=\dfrac{1}{2}\Rightarrow \dfrac{KI}{KA}=\dfrac{3}{4}$
$\Rightarrow \dfrac{IG}{AC}=\dfrac{3}{4}\Rightarrow \dfrac{d(I,(SCD))}{d(A,(SCD))}=\dfrac{3}{4}\Rightarrow AH=\dfrac{4}{3}.\dfrac{3a\sqrt3}{8}=\dfrac{a\sqrt3}{2}$
$AC=\sqrt{AD^2-CD^2}=a\sqrt3$
Ta có: $\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow SA=a$
$V_{SABCD}=\dfrac{1}{3}SA.S_{ABCD}=\dfrac{a^3\sqrt3}{4}$
b) Ta có: $BC//AD\Rightarrow \dfrac{AO}{OC}=\dfrac{OD}{OB}=\dfrac{AD}{BC}=2$
$\Rightarrow AO=\dfrac23AC=\dfrac{2a\sqrt3}{3}$
$SO=\sqrt{SA^2+AO^2}=\dfrac{\sqrt{21}}{3}$
Qua $O$ kẻ đường thẳng song song với $AD$ cắt $CD$ tại $M$
$\Rightarrow \dfrac{OM}{BC}=\dfrac{OD}{BD}=\dfrac23\Rightarrow OM=\dfrac23a$
$\dfrac{CM}{CD}=\dfrac{OB}{BD}=\dfrac13\Rightarrow CM=\dfrac13a$
$AM=\sqrt{AC^2+CM^2}=\dfrac{2a\sqrt7}{3}$
$SM=\sqrt{AM^2+SA^2}=\dfrac{a\sqrt{37}}{3}$
$\cos \widehat{SOM}=\dfrac{OS^2+OM^2-SM^2}{2OSOM}=\dfrac{-\sqrt{21}}{7}$
$\Rightarrow (SO,AD)=(SO,OM)=\arccos \dfrac{\sqrt{21}}{7}$
Có gì khúc mắc bạn hỏi lại nhé <3
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


