View attachment 26107
$\begin{array}{l}
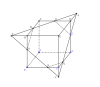
D'P = KB' = \frac{a}{2}\\
\frac{{D'P}}{{DQ}} = \frac{{D'E}}{{DE}} = \frac{5}{7} \Rightarrow DQ = \frac{{7D'P}}{5} = \frac{{7a}}{{10}} \Rightarrow \frac{{CQ}}{{DQ}} = \frac{3}{7}\\
\frac{{CF}}{{ED}} = \frac{{CQ}}{{DQ}} = \frac{3}{7} \Rightarrow CF = \frac{3}{7}ED = \frac{a}{4}\\
B'H = D'E = \frac{5}{{12}}a\\
CG = CQ = \frac{{3a}}{{10}}\\
{V_H} = {V_{C'KPF}} - {V_{KB'HM}} - {V_{PD'NE}} - {V_{FGCQ}}\\
= \frac{1}{3}\frac{1}{2}{\left( {\frac{{3a}}{2}} \right)^2}\frac{{5a}}{4} - \frac{1}{3}\frac{1}{2}\frac{a}{2}\frac{{5a}}{{12}}\frac{a}{2} - \frac{1}{3}\frac{1}{2}\frac{a}{2}\frac{{5a}}{{12}}\frac{a}{2} - \frac{1}{3}\frac{1}{2}{\left( {\frac{{3a}}{{10}}} \right)^2}\frac{a}{4} = \frac{{1549{a^3}}}{{3600}}
\end{array}$
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.