mọi người giúp em hai câu này với ạ, em làm không ra
(
Bài 9:
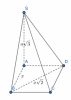
Đặt $AB=x \implies BD=x\sqrt2$ ($ABCD$ là hình vuông)
Vì $\triangle SBD$ là tam giác đều nên $SB=BD=x\sqrt2$
Xét $\triangle SAB $ vuông tại $A$ ta có
$SA^2+AB^2=SB^2$
thay số vào tìm được $x=a\sqrt3$
$\implies AB=a\sqrt3$
$V_{S.ABCD}=\dfrac{1}3\cdot SA.S_{ABCD}$
Bài 11
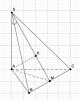
Gọi $M$ là trung điểm $BC$
Xét $\triangle SAM $ kẻ $AK \perp SM$
$\implies \widehat{(SA;(SBC))}=\widehat{ASK}=\widehat{ASM}$
Ta có $\tan \widehat{ASM}=\dfrac{AM}{SA}$
Với $AM=\dfrac{a\sqrt3}{2}$ (Vì $ABC$ đều)
Đến đây em tìm $SA$ là ra thể tích nha
Có chỗ nào chưa hiểu hỏi lại nhé em
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
