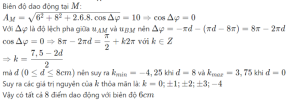[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Trên mặt nước tại hai điểm S1 S2 cách nhau 8 cm, người ta đặt 2 nguồn sóng cơ kết hợp, dao động điều hòa theo phương thẳng đứng với phương trình [imath]u_{A}=6cos(40 \pi t)[/imath] và [imath]u_{B}=8cos(40\pi t)[/imath] (uA và uB tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt nước là 40 (cm/s), coi biên độ sóng không đổi khi truyền đi. Trên đoạn thẳng S1S2, tính số điểm dao động với biên độ bằng 6 cm.
Mọi người giúp em bài này với ạ, đề cho 2 cái biên độ khác nhau nên em chưa nghĩ ra cách làm ạ, em xin cảm ơn.
Mọi người giúp em bài này với ạ, đề cho 2 cái biên độ khác nhau nên em chưa nghĩ ra cách làm ạ, em xin cảm ơn.