Toán 9 Tính PH theo R, tìm min A

[hobao281005@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho (O;R) và dây cung AB(AB<2R) trên tia AB lấy C sao cho AC>AB. Từ C kẻ 2 tiếp tuyến CP, CK(P thuộc cung nhỏ AB;P, K là tiếp điểm). Gọi I là trung điểm AB

Tiếp tuyến màu tím
Đường cao ΔCPK là màu đỏ
OI màu xanh là trung tuyến ΔOAB

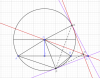
a)C/m tgiác CIOK nội tiếp
C/m tam giác OAB cân ở O có I là trung điểm AB
=>OI vuông AB
mà $\widehat{CKI}=90^o$(CK là tiếp tuyến)
=>tgiác CIOK nội tiếp
b)C/m $CP^2=AC.BC$
Xét ΔCPB, ΔCAP có
$\widehat{ACP}$ chung
$\widehat{CPB}=\widehat{CAP}$(góc tạo bởi tia tiếp tuyến và dây cung cùng chắn góc nội tiếp cung BP)
=>ΔCPB $\sim$ ΔCAP(g.g)
=>$\frac{CP}{CA}=\frac{CB}{CP}$<=>$CP^2=AC.BC$
c)Gọi H là trực tâm ΔCPK. Tính PH theo R
2)Tìm min $A=x^2-5x+\frac{9}{x}+2017$(x>0)
Giúp mình phần c và bài 2 với
Phần mềm vẽ hình: GeoGebra

 

[7 1 2 5]

c) Ta có: [tex]\left\{\begin{matrix} PH\perp KC\\ KH\perp PC \end{matrix}\right.\Rightarrow \left\{\begin{matrix} PH//OK\\ KH//OP \end{matrix}\right.\Rightarrow[/tex] PHKO là hình bình hành [TEX]\Rightarrow PH=OK=R[/TEX]
2) [tex]A=x^2-5x+\frac{9}{x}+2017=(x^2+9)-5x+\frac{9}{x}+2008\geq 6x-5x+\frac{9}{x}+2008=x+\frac{9}{x}+2008\geq 2\sqrt{x.\frac{9}{x}}+2008=6+2008=2014[/tex]
Dấu "=" xảy ra khi x = 3.

 

[hobao281005@gmail.com]

c) Ta có: [tex]\left\{\begin{matrix} PH\perp KC\\ KH\perp PC \end{matrix}\right.\Rightarrow \left\{\begin{matrix} PH//OK\\ KH//OP \end{matrix}\right.\Rightarrow[/tex] PHKO là hình bình hành [TEX]\Rightarrow PH=OK=R[/TEX]
2) [tex]A=x^2-5x+\frac{9}{x}+2017=(x^2+9)-5x+\frac{9}{x}+2008\geq 6x-5x+\frac{9}{x}+2008=x+\frac{9}{x}+2008\geq 2\sqrt{x.\frac{9}{x}}+2008=6+2008=2014[/tex]
Dấu "=" xảy ra khi x = 3.

2)
$A=x^2-5x+\frac{9}{x}+2017=x^2+9-6x+\frac{9}{x}+x+2008=(x-3)^2+x+\frac{9}{x}+2008$
Áp dụng BĐT côsi với 2 số dương x,$\frac{9}{x}$
$=>x+\frac{9}{x}+2008\geq 2\sqrt{x.\frac{9}{x}}+2008=6+2008=2014$
mà $(x-3)^2\geq 0 với \forall x>0$
$=>x+\frac{9}{x}+2008+(x-3)^2\geq 2014$
Vậy min A=2014 khi $ \left\{\begin{matrix} x=\frac{9}{x}\\(x-3)^2=0 \end{matrix}\right.$
$<=>x=3$