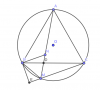
View attachment 65318
+) Trên AM lấy điểm N sao cho MN=MB
Ta có [tex]\widehat{BMA}=\widehat{BCA}=60^{\circ}[/tex] nên [tex]\Delta BMN[/tex] đều
[tex]\Rightarrow BN=BM[/tex]
Mặt khác:
- [tex]BA=BC[/tex]
- [tex]\widehat{BMC}+\widehat{CMN}=\widehat{ABN}+\widehat{CMN}(=60^{\circ})\Rightarrow[COLOR=#ff0000]\widehat{BMC}= \widehat{ABN}[/COLOR][/tex]
[tex]\Rightarrow \Delta ABN=\Delta CBM(c-g-c)\Rightarrow AN=MC[/tex]
[tex]MA=MN+NA=MB+MC\Rightarrow MA^2=(MB+MC)^2=MB^2+MC^2+2MB.MC[/tex]
+)Từ B hạ [tex]BE\perp MN[/tex] tại E
Vì tứ giác ABMC nội tiếp nên [tex]\widehat{BMC}+\widehat{BAC}=180^{\circ}\Rightarrow \widehat{BMC}=120^{\circ}\Rightarrow \widehat{BME}=60^{\circ}[/tex]
[tex]\cos \widehat{BME}=\frac{ME}{BM}\Leftrightarrow \frac{1}{2}=\frac{ME}{BM}\Leftrightarrow BM=2ME[/tex]
Theo định lý Pythagores ta có:
[tex]BC^2=BE^2+EC^2=BE^2+(EM+MC)^2=BE^2+EM^2+2EM.MC+MC^2=BM^2+MC^2+MB.MC[/tex]
Xét: [tex]MA^{2}+MB^{2}+MC^{2}=(MB+MC)^2+MB^{2}+MC^{2}=2(MB^{2}+MC^{2}+MB.MC)=2BC^2[/tex]
Việc còn lại là tính [tex]BC^2[/tex] theo R, bạn có thể làm được, chú ý là tam giác ABC đều và nội tiếp (O;R)
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.