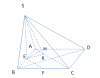
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E, F là trung điểm AB, BC. Tính khoảng cách hai đường thẳng SA, EF?
Mọi người giúp em ạ
Nối A với C, B với D.
EF không thuộc (SAC), EF//AC => EF// (SAC) => khoảng cách giữa SA và EF là khoảng cách giữa EF và (SAC).
Nối S với E. Kẻ EK vuông góc AC. Nối S với K. Kẻ EH vuông góc SK.
Tam giác SAB đều => SE vuông góc với AB. Mà (SAB) vuông góc (ABCD) => SE vuông góc (ABCD) => SE vuông góc AC.
AC vuông góc EK, AC vuông góc SE => AC vuông góc (SEK) => (SEK) vuông góc (SAC).
EH thuộc (SEK), EH vuông góc với giao tuyến SK của (SEK) và (SAC) => EH vuông góc (SAC). Mà EF// (SAC) => EH vuông góc EF => EH là khoảng cách giữa EF và (SAC) hay khoảng cách giữa EF và SA.
Tam giác SEK vuông tại E (SE vuông góc EK) => SE.EK=EH.SK.
Thay SE=1/2.a.căn 3, EK=1/4.a.căn 2, SK=a.(căn 7)/(căn 8) => EH=1/14.a.căn 21.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.