leduymanh2005
Câu 4:
[imath]a/[/imath]
Khoảng cách [imath]2[/imath] cực đại liên tiếp trên đoạn nối hai nguồn là [imath]\dfrac{\lambda}{2}=2 \Rightarrow \lambda = 4cm[/imath]
[imath]b/[/imath]
[imath]M[/imath] là điểm cực đại cùng pha với hai nguồn nên ta có:
[imath]MA-MB=m\lambda[/imath]
[imath]MA+MB=n\lambda[/imath]
với [imath]m,n[/imath] là số nguyên cùng chẵn hoặc cùng lẻ
Theo đề ra, [imath]m=1[/imath] là số lẻ nên [imath]n[/imath] cũng là số lẻ.
VÌ trên [imath]AB[/imath] có [imath]15[/imath] cực đại nên suy ra [imath]7\lambda \le AB<8\lambda[/imath]
Theo bất đẳng thức tam giác: [imath]MA+MB = n\lambda > AB[/imath]
Suy ra [imath]n=9[/imath]
hay: [imath]MA+MB=9\lambda = 36cm[/imath]
kết hợp với [imath]MA-MB=\lambda = 4cm[/imath]
Tìm được [imath]MA=20cm;MB=16cm[/imath]
Định lí hàm số [imath]\cos[/imath] trong tam giác [imath]MAB[/imath] có góc [imath]B[/imath] bằng [imath]60^{\circ}[/imath]
[imath]MA^2=AB^2+MB^2-2.AB.MB.\cos 60[/imath]
[imath]\Rightarrow AB\approx 22,42cm[/imath] | 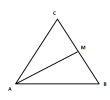 |
Chúc bạn học tốt!
-----
Xem thêm:
Tổng hợp những điều quan trọng trong chương Sóng cơ
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.