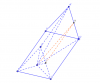
Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Tính góc giữa hai mặt phẳng (GB’C’) và (ABC)
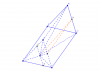
Qua $G$ vẽ đường thằng song song với $A'C'$; cắt $AB$ và $BC$ lần lượt tại $D;E$.
$DE= (GC'A') \cap (ABC)$.
Lấy $H$ là trung điểm $A'C' ;I$ là trung điểm $AC=> IH//AA'//CC'=> IH \perp (ABC)=> IH \perp IG$
$\Delta ABC$ đều nên $BI \perp AC=> GI \perp DE$(1).
Do $\Delta ABC$ đều $=> GA=GC=> \sqrt{AA'^2+GA^2}=\sqrt{CC'+ GC^2}$ hay $GA'=GC'=> \Delta GA'C'$ cân
$=> GH \perp A'C'=> GH \perp DE$(2).
Từ (1) và (2) $=> (\widehat{(GA'C'),(ABC)})=\widehat{HGI}$.
Xét $\Delta GIH$ có $HI \perp IG=> \Delta GIH$ vuông tại I.
Tính được:$ GI=\frac{1}{3}.BI=\frac{1}{3}.\frac{\sqrt{3}.a}{2}=\frac{\sqrt{3}.a}{6}$
$=> tan \widehat{HGI}=\frac{IH}{IG}=\frac{a}{\frac{\sqrt{3}.a}{6}}=2 \sqrt{3}=>\widehat{HGI} \approx 73.89^o$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
