Toán 12 Tính đơn điệu của hàm số

[10112003mailinh@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho mình hỏi bài này trình bày tự luận kiểu gì ạh? Mình cảm ơn

 

[Kaito Kidㅤ]

[tex]g'(x)=2xf'(x^2-2)\\g'(x)=0\Leftrightarrow \left[\begin{array}{l} x=0\\x^2-2=-1\\x^2-2=-2 \end{array}\right.\Leftrightarrow \Leftrightarrow \left[\begin{array}{l} x=0\\x=\pm 1\\x= \pm 2 \end{array}\right.[/tex]
Xét dấu $g'(x)$:

Chọn A

 

[10112003mailinh@gmail.com]

[tex]g'(x)=2xf'(x^2-2)\\g'(x)=0\Leftrightarrow \left[\begin{array}{l} x=0\\x^2-2=-1\\x^2-2=-2 \end{array}\right.\Leftrightarrow \Leftrightarrow \left[\begin{array}{l} x=0\\x=\pm 1\\x= \pm 2 \end{array}\right.[/tex]
Xét dấu $g'(x)$:
View attachment 162694
Chọn A

mình chưa hiểu phần xét dấu ạh

 

[Kaito Kidㅤ]

mình chưa hiểu phần xét dấu ạh

Ủa dễ mà anh :v
Xét x>2 thì chị chọn bừa số nào >2 rồi thay vào, em lấy số 3
[tex]g'(3)=2.3.f'(3^2-2)=6.f'(7)[/tex]
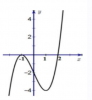
Nhìn vào đồ thị của $f'(x)$ thấy $f'(7)>0$ nên $g'(3)>0$ Do đó $g'(x)$ mang dấu dương
Với $0<x<1$ em lấy [tex]x=\frac{1}{2}[/tex] đi
$g'(\frac{1}{2})=2.\frac{1}{2}.f'(\frac{1}{4}-2)=f'(\frac{-7}{4})$
Nhìn vào đồ thị thấy $f'(\frac{-7}{4}) <0$ nên TH này $g'(x)$ mang dấu âm
Các TH còn lại tương tự