[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
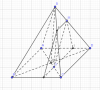
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tất cả các cạnh bên đều bằng a. Gọi điểm M thuộc cạnh SD sao cho SD=3SM, điểm G là trọng tâm tam giác BCD. Gọi $(\alpha)$ là mặt phẳng chứa MG và song song với CD. Diện tích thiết diện thu được khi mặt phẳng $(\alpha)$ cắt hình chóp bằng
Câu này làm như nào ạ!
Câu này làm như nào ạ!
Attachments
Last edited by a moderator: