Vật lí 12 tính chu kì cld

[leduymanh2005]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

mn giúp mik câu này vs

 

[Hoàng Long AZ]

mn giúp mik câu này vsView attachment 218306

leduymanh2005
[imath]a/[/imath]
[imath]\alpha_m = 9^{\circ}=\dfrac{\pi}{20} \ rad[/imath]
[imath]A=\alpha _m .l = \dfrac{\pi}{20}m[/imath]
[imath]\omega = \sqrt{\dfrac{g}{l}}=\pi \ rad/s[/imath]
[imath]t=0[/imath] là lúc vật qua vị trí cân bằng theo chiều âm
Vậy phương trình li độ dài: [imath]x=\dfrac{\pi}{20}\cos (\pi t +\dfrac{\pi}{20})m[/imath]
[imath]b/[/imath]

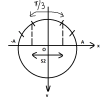
Trong quãng thời gian [imath]\Delta t[/imath], góc quét là: [imath]\Delta \varphi = \omega . \Delta t = \pi + \dfrac{\pi}{3} \ rad[/imath] Quãng đường đi được khi quét được cung [imath]\pi[/imath] là: [imath]S_1 = 2A=\dfrac{\pi}{10}m[/imath] Để quãng đường đi trong thời gian [imath]\Delta t[/imath] lớn nhất thì quãng đường đi khi quét cung [imath]\dfrac{\pi}{3}[/imath] là lớn nhất. Vậy phải đi trong vùng có vận tốc lớn nhất, do đó lấy đối xưng cung [imath]\dfrac{\pi}{3}[/imath] qua trục [imath]Ov[/imath] như hình vẽ khi đó: [imath]S_2=\dfrac{2.A}{2}=\dfrac{\pi}{20}m[/imath] Vậy quãng đường đi lớn nhất trong thời gian [imath]\Delta t[/imath]: [imath]S=S_1+S_2=\dfrac{3\pi}{20}m[/imath]

[imath]c/[/imath]

Khi cân bằng, ta có hình vẽ bên [imath]P=mg = 0,2N[/imath] [imath]F_d=qE=0,2N[/imath] Theo phương Oy ta có: [imath]T\cos \varphi =P+F_d \cos 30[/imath] [imath]T\sin \varphi = F_d\sin 30[/imath] [imath]\Rightarrow \tan \varphi = 2-\sqrt{3} \Rightarrow \varphi = 15^{\circ}[/imath] + Gọi [imath]g'[/imath] là gia tốc trọng trường biểu kiến Định lí hàm số [imath]\cos[/imath] [imath]g'^2 =g^2 + (\dfrac{F_d}{m})^2 +2g\dfrac{F_d}{m}\cos30[/imath] [imath]\Rightarrow g' \approx 19,3 m/s^2[/imath] Chu kì dao động: [imath]T=2\pi \sqrt{\dfrac{l}{g'}} \approx 1,43s[/imath]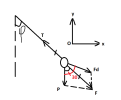

Chúc bạn học tốt!
------
Xem thêm: Hệ thống toàn bộ công thức vật lí 12