- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Kiến thức cơ bản:
Cho hàm f(x) liên tục trên (a;b). Với [TEX]x_o[/TEX] thuộc (a;b), sao cho [TEX]f'(x_o)=0[/TEX]. Ta có :
[TEX]f(x)[/TEX] đạt cực đại tại [TEX]x_o[/TEX] nếu [TEX]f''(x_o)<0[/TEX]
[TEX]f(x)[/TEX] đạt cực tiểu tại [TEX]x_o[/TEX] nếu [TEX]f''(x_o)>0[/TEX]
Nếu [TEX]f''(x_o)=0[/TEX] thì ta chưa kết luận được, phải xét cực đại, cực tiểu bằng phương pháp khác ( lập BBT xét dấu)
Đây là kiến thức cơ bản trong SGK, ta có tính chất mở rộng như sau:
Cho hàm f(x) liên tục trên (a;b). Với [TEX]x_o[/TEX] thuộc (a;b), sao cho [TEX]f'(x_o)=0[/TEX]. Ta có :
[TEX]f^{(n)}(x_o)>0[/TEX](đạo hàm cấp n của f(x), với n chẵn) thì f(x) đạt cực tiểu tại [TEX]x_o[/TEX]
[TEX]f^{(n)}(x_o)<0[/TEX](đạo hàm cấp n của f(x), với n chẵn) thì f(x) đạt cực đại tại [TEX]x_o[/TEX]
[TEX]f^{(n)}(x_o)=0[/TEX] thì ta cũng chưa kết luận được, và phải dùng xét dấu.
Lưu ý là đạo hàm cấp n phải chẵn, các điều kiện sau thì giống hệt với đạo hàm cấp 2. Cho nên các bạn có thể nhớ đạo hàm cấp 2, có 2 là số chẵn, để suy ra đạo hàm cấp n thì n cũng phải chẵn.
Với tính chất mở rộng này, ta có thể giải các bài toán biện luận tham số m để hàm đạt CĐ, CT tại [TEX]x=x_o[/TEX], khi mà [TEX]f''(x_o)=0[/TEX]
Có bao nhiêu giá trị nguyên của m để hàm số: [TEX]y=mx^8+2mx^6+(m^2-2m-3)x^4[/TEX] đạt cực đại tại x=0?
Giải: Ta có: [TEX]y'=8mx^7+12mx^5+4(m^2-2m-3)x^3[/TEX]
[TEX]y''=56mx^6+60mx^4+12(m^2-2m-3)x^2[/TEX]
Ta có thể thấy [TEX]y''(0)=0[/TEX], chưa thể kết luận được, nên cần dùng định lý mở rộng.
Ta thấy đạo hàm đến cấp 4 thì số hạng thứ 3 sẽ mất x đi và chỉ còn tham số m, như vậy khi thay x=0 thì biểu thức có thể khác 0. Các hệ số bên tự do ( không gồm tham số m) thì không quan trọng đến việc biện luận, nên ta có thể bỏ qua.
Ta có: [TEX]y^{(4)}(0)=m^2-2m-3[/TEX]
Để x=0 là CĐ thì [TEX]y^{(4)}(0)<0<=>m^2-2m-3<0<=>-1<m<3[/TEX]
Xét các trường hợp [TEX]y^{(4)}(0)=0[/TEX]<=>m=-1 hoặc m=3
Với m=-1 có [TEX]y'=-8x^7-12x^5=x^5(-8x^2-12)[/TEX]
Lập BBT dễ thấy khi qua x=0 thì y' đổi dấu từ + sang -. Nên với m=-1 thì x=0 là cực đại, thỏa mãn.
Với m=3 có [TEX]y'=24x^7+36x^5=x^5(24x^2+36)[/TEX]
Khi qua x=0 thì y' đổi dấu từ - sang +, vậy x=0 là cực tiểu, không thỏa mãn.
Vậy có 4 giá trị của m thỏa mãn là -1,0,1,2
Vậy câu hỏi đặt ra là nếu như số hạng chứa x với mũ nhỏ nhất là mũ lẻ, dẫn đến đạo hàm cấp n lẻ thì sao? Thì yên tâm câu hỏi dạng này họ sẽ để chẵn.
Có thể kiểm nghiệm với m=1, và [TEX]y=x^8+2x^6-4x^4[/TEX]
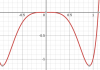
Đồ thị được biểu diễn như hình trên, có thể thấy x=0 đúng là cực đại. Tuy nhiên nếu là:
[TEX]y=x^8+2x^6-4x^5[/TEX] ( số hạng có x mũ nhỏ nhất là mũ lẻ) thì x=0 không là cực trị
Cho hàm f(x) liên tục trên (a;b). Với [TEX]x_o[/TEX] thuộc (a;b), sao cho [TEX]f'(x_o)=0[/TEX]. Ta có :
[TEX]f(x)[/TEX] đạt cực đại tại [TEX]x_o[/TEX] nếu [TEX]f''(x_o)<0[/TEX]
[TEX]f(x)[/TEX] đạt cực tiểu tại [TEX]x_o[/TEX] nếu [TEX]f''(x_o)>0[/TEX]
Nếu [TEX]f''(x_o)=0[/TEX] thì ta chưa kết luận được, phải xét cực đại, cực tiểu bằng phương pháp khác ( lập BBT xét dấu)
Đây là kiến thức cơ bản trong SGK, ta có tính chất mở rộng như sau:
Cho hàm f(x) liên tục trên (a;b). Với [TEX]x_o[/TEX] thuộc (a;b), sao cho [TEX]f'(x_o)=0[/TEX]. Ta có :
[TEX]f^{(n)}(x_o)>0[/TEX](đạo hàm cấp n của f(x), với n chẵn) thì f(x) đạt cực tiểu tại [TEX]x_o[/TEX]
[TEX]f^{(n)}(x_o)<0[/TEX](đạo hàm cấp n của f(x), với n chẵn) thì f(x) đạt cực đại tại [TEX]x_o[/TEX]
[TEX]f^{(n)}(x_o)=0[/TEX] thì ta cũng chưa kết luận được, và phải dùng xét dấu.
Lưu ý là đạo hàm cấp n phải chẵn, các điều kiện sau thì giống hệt với đạo hàm cấp 2. Cho nên các bạn có thể nhớ đạo hàm cấp 2, có 2 là số chẵn, để suy ra đạo hàm cấp n thì n cũng phải chẵn.
Với tính chất mở rộng này, ta có thể giải các bài toán biện luận tham số m để hàm đạt CĐ, CT tại [TEX]x=x_o[/TEX], khi mà [TEX]f''(x_o)=0[/TEX]
Có bao nhiêu giá trị nguyên của m để hàm số: [TEX]y=mx^8+2mx^6+(m^2-2m-3)x^4[/TEX] đạt cực đại tại x=0?
Giải: Ta có: [TEX]y'=8mx^7+12mx^5+4(m^2-2m-3)x^3[/TEX]
[TEX]y''=56mx^6+60mx^4+12(m^2-2m-3)x^2[/TEX]
Ta có thể thấy [TEX]y''(0)=0[/TEX], chưa thể kết luận được, nên cần dùng định lý mở rộng.
Ta thấy đạo hàm đến cấp 4 thì số hạng thứ 3 sẽ mất x đi và chỉ còn tham số m, như vậy khi thay x=0 thì biểu thức có thể khác 0. Các hệ số bên tự do ( không gồm tham số m) thì không quan trọng đến việc biện luận, nên ta có thể bỏ qua.
Ta có: [TEX]y^{(4)}(0)=m^2-2m-3[/TEX]
Để x=0 là CĐ thì [TEX]y^{(4)}(0)<0<=>m^2-2m-3<0<=>-1<m<3[/TEX]
Xét các trường hợp [TEX]y^{(4)}(0)=0[/TEX]<=>m=-1 hoặc m=3
Với m=-1 có [TEX]y'=-8x^7-12x^5=x^5(-8x^2-12)[/TEX]
Lập BBT dễ thấy khi qua x=0 thì y' đổi dấu từ + sang -. Nên với m=-1 thì x=0 là cực đại, thỏa mãn.
Với m=3 có [TEX]y'=24x^7+36x^5=x^5(24x^2+36)[/TEX]
Khi qua x=0 thì y' đổi dấu từ - sang +, vậy x=0 là cực tiểu, không thỏa mãn.
Vậy có 4 giá trị của m thỏa mãn là -1,0,1,2
Vậy câu hỏi đặt ra là nếu như số hạng chứa x với mũ nhỏ nhất là mũ lẻ, dẫn đến đạo hàm cấp n lẻ thì sao? Thì yên tâm câu hỏi dạng này họ sẽ để chẵn.
Có thể kiểm nghiệm với m=1, và [TEX]y=x^8+2x^6-4x^4[/TEX]
Đồ thị được biểu diễn như hình trên, có thể thấy x=0 đúng là cực đại. Tuy nhiên nếu là:
[TEX]y=x^8+2x^6-4x^5[/TEX] ( số hạng có x mũ nhỏ nhất là mũ lẻ) thì x=0 không là cực trị
