Tính chất các đường đồng quy trong tam giác

[minhmai2002]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

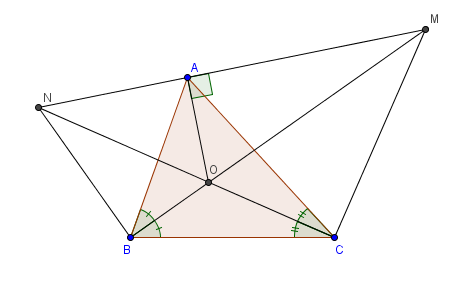
Đề bài: cho [tex]\large\Delta \ ABC[/tex] các tia phân giác của [TEX]\widehat{B}[/TEX] và [TEX]\widehat{C}[/TEX] cắt nhau tại O. Từ A vẽ đường thẳng vuông góc với OA cắt các tia BO và CO lần lượt tại M và N. Chứng minh rằng:
a, BM[TEX]\perp \[/TEX]BN
b, CM[TEX]\perp \[/TEX]CN

 

[iceghost]

Ở đây ta áp dụng các tính chất về tia phân giác nhé
+ Đường phân giác ngoài và phân giác trong của một góc thì luôn vuông góc với nhau
+ Giao điểm của hai tia phân giác của hai góc ngoài bất kì trong tam giác thì nằm trên tia phân giác góc trong của góc còn lại

a) Xét $\triangle$ ABC có :
BM là đường phân giác thứ nhất (gt)
CN là đường phân giác thứ hai (gt)
Mà O là giao điểm của BM và CN
$\implies$ AO là đường phân giác thứ ba
Mà MN $\perp$ AO ( gt )
$\implies$ MN là tia phân giác góc ngoài A
Mà CN là tia phân giác góc trong C
$\implies$ BN là tia phân giác góc ngoài B
Mà BM là tia phân giác góc trong B
$\implies$ BM $\perp$ BN

b) Xét $\triangle$ ABC có :
MN là tia phân giác góc ngoài A
Mà BM là tia phân giác góc trong B
$\implies$ CM là tia phân giác góc ngoài C
Mà CN là tia phân giác góc trong C
$\implies$ CM $\perp$ CN