b,
Tính BC => BK,KC
Có AB,BK => AK
Có AK,KC,AC dùng công thức [tex]S=\frac{1}{2}.AB.KC=\frac{AC.KC.AK}{4R}[/tex]
Dùng định lí cos tính cosAKC
c,
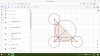
Tưởng tượng cái hình sẽ kiểu thế này
Khi 2 đường tròn giao nhau thì đường nối tâm sẽ là đường trung trực của dây chung
Với trường hợp giao nhau tại 1 điểm thì điểm đó nằm trên đường nối tâm
Hay:
A,D,G thẳng hàng
B,E,G thẳng hàng
C,F,G thẳng hàng
Gọi bán kính (C) = b
Xét tam giác BGC:
[tex]\frac{GE}{EB}=\frac{GF}{FC} \ (=\frac{b}{a})[/tex]
=> EF//BC
Tương tự DE//AB
mà AB vuông BC
=> EF vuông DE
=> DF đường kính
=> G thuộc DF
Mà A,D,G thẳng hàng, C,F,G thẳng hàng
=> A,D,F,G,C thẳng hàng hay G thuộc AC
Ta có:
AG=AD+DG=a+b
CG=CF+FG=a+b
=> AG=CG
=> G trung điểm AC
Có: [tex]AC=AG+CG=2(a+b)=5a\sqrt{2}[/tex]
=> b=....
Lâu lắm rồi mới làm hình 9 :<
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
giúp mình câu 2b ,c với t2 thi r huhu
