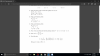
16. Tìm $x$ để $1 \le \dfrac{2x+4}{x-5} \le 3$
17. Cho biểu thức $A =\left[ \dfrac{5}{x+3} - \dfrac{5x-15}{2x-9}\left(\dfrac{2x-9}{x^2-9} - 2x+9 \right)\right]: \dfrac{1-x}{1+x}$
Rút gọn $A$ và tìm $x$ để $A<0$
mn giúp em vs ạ bài số 16 và 17 ạ . gấp nhé mn ơi
16.
$1 \le \dfrac{2x+4}{x-5} \le 3\\ \implies \begin{cases} 1\le \dfrac{2x+4}{x-5} \\ \dfrac{2x+4}{x-5} \le 3 \end{cases}\\ \implies \begin{cases} \dfrac{2x+4}{x-5} -1 \ge 0 \\ \dfrac{2x+4}{x-5} -3 \le 0 \end{cases} \\ \implies \begin{cases} \dfrac{2x+4 - x+5 }{x-5} \ge 0 \\ \dfrac{2x+4 -3x+15}{x-5} \le 0 \end{cases} \\ \implies \begin{cases} \dfrac{x+9}{x-5} \ge 0 \\ \dfrac{16-x}{x-5} \le 0 \end{cases} \\ \implies \begin{cases} \left[ \begin{array}{I} x>5 \\ x \le -9 \end{array}\right. \\ \left[\begin{array}{I} x < 5 \\ x \ge 19 \end{array}\right. \end{cases} \\ \implies \left[ \begin{array}{I} x \le -9 \\ x \ge 19 \end{array}\right. $
Vậy $\left[ \begin{array}{I} x \le -9 \\ x \ge 19 \end{array}\right.$ để $1 \le \dfrac{2x+4}{x-5} \le 3$
17.
a.
$\begin{aligned} A & =\left[ \dfrac{5}{x+3} - \dfrac{5x-15}{2x-9}\left(\dfrac{2x-9}{x^2-9} - 2x+9 \right)\right]: \dfrac{1-x}{1+x} \\ & = \left[ \dfrac{5}{x+3} - \dfrac{5(x-3)}{2x-9} \cdot \dfrac{2x-9}{(x-3)(x+3)} + \dfrac{5(x-3)}{2x-9} \cdot (2x-9) \right] :\dfrac{1-x}{1+x} \\ & = \dfrac{5(x-3)(x+1)}{1-x}\end{aligned} $
b.
Ta có: $\dfrac{5(x-3)(x+1)}{1-x} < 0 \iff \left[\begin{array}{I} \begin{cases}5(x-3)(x+1) > 0 \\ 1-x <0 \end{cases} \\ \begin{cases} 5(x-3)(x+1) < 0 \\ 1-x >0 \end{cases} \end{array}\right. \implies \left[ \begin{array}{I} x >3 \\ -1<x<1 \end{array}\right.$
Vậy $\left[ \begin{array}{I} x >3 \\ -1<x<1 \end{array}\right.$ để $A < 0$
Có gì không hiểu em hỏi lại nhé. Chúc em học tốt
Ngoài ra em có thể tham khảo thêm kiến thức tại link này nha:
https://diendan.hocmai.vn/threads/tong-hop-topic-on-thi-hoc-ki.841342/
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
