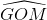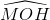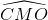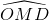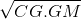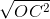Toán 9 Tìm vị trí của M

[VTR♚Shiro♛]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

( Giúp mình phần c với ạ, phần a,b mình làm rồi)
Cho đường tròn (O; R) và đường thẳng d không đi qua O cắt đường tròn tại hai điểm A và B. Lấy một điểm M trên tia đối của tia BA (M ≠ B), vẽ hai tiếp tuyến MC và MD với đường tròn (O), (C, D là các tiếp điểm). Gọi E là trung điểm của AB và I là giao điểm của CD và OM.
a. Chứng minh 5 điểm O, E, C, D, M cùng thuộc một đường tròn.
b. Chứng minh rằng: MI . MO = MB . MA
c. Đường thẳng d’ đi qua O và vuông góc với OM cắt các tia MC, MD theo thứ tự tại G và H. Tìm vị trí của điểm M trên đường thẳng d sao cho diện tích tam giác MGH bé nhất.

 

[Bangtanbomm]

Xét ∆MOG và ∆MOH có

=

= 90° (d’ ⊥ OM)
OM là cạnh chung

=

(do ∆MCO = ∆MDO)
Nên ∆MOG = ∆MOH
S∆MGH = 2S∆MGO = 2[tex]\frac{OC.GM}{2}[/tex]= OC.GM
S∆MGH đạt giá trị nhỏ nhất khi GM nhỏ nhất
GM = CG + CM > 2

= 2

= 2OC
Vậy GM đạt giá trị nhỏ nhất là 2OC khi CG = CM Khi đó ∆OCM vuông cân tại C
[tex]OM=OC\sqrt{2}=R\sqrt{2}[/tex]
Vậy vị trí điểm M cần tìm (trên tia đối của tia BA) là giao điểm của đường thẳng d với đường tròn tâm O bán kính bằng
[tex]R\sqrt{2}[/tex]