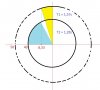
Ở hình bên, một lò xo nhẹ, có độ cứng k=4,8N/m được gắn một đầu cố định vào tường để lò xo nằm ngang. Một xe lăn, khối lượng M=0,2kg và một vật nhỏ có khối lượng m=0,1kg nằm yên trên xe, đang chuyển động dọc theo trục của lò xo với vận tốc v=20cm/s, hướng đến lò xo. Hệ số ma sát nghỉ cực đại bằng hệ số ma sát trượt giữa vật nhỏ và xe là μ=0,04. Bỏ qua ma sát giữa xe và mặt sàn, coi xe đủ dài để vật không rời khỏi xe, lấy g=10m/s2. Thời gian từ khi xe bắt đầu chạm lò xo đến khi lò xo nén cực đại gần nhất với giá trị nào sau đây?
A. 0,345s
B. 0,361s
C. 0,513s
D. 0,242s
Phân tích một xíu để bạn có thể theo dõi hướng giải quyết của mình ha:
+ Lúc đầu, xe va chạm với lò xo va dao động. Lúc này xe và vật nhỏ xem như một vật có khối lượng là M+m.
+ Đến một "lúc nào đó" thì lực ma sát nghỉ giữa 2 vật cực đại và vật nhỏ trượt trên xe. Lúc này xe chịu tác dụng của lực ma sát trượt.
+ Tại thời điểm vật nhỏ bắt đầu trượt trên xe thì hệ dao động không còn chứa vật nhỏ nữa, hệ dao động chỉ còn lại xe và lò xo.
+ Năng lượng của hệ tại thời điểm vật nhỏ trượt sẽ chuyển thành năng lượng lúc lò xo nén cực đại + công của lực ma sát.
+ Thời gian vật đi = thời gian từ lúc va chạm đến lúc vật nhỏ trượt + thời gian từ lúc vật nhỏ trượt đến lúc lò xo nén cực đại
Mình sẽ giải quyết từng ý nhỏ.
+ Lúc xe và lo xo va chạm, vận tốc của hệ lúc đó là v = 20cm/s. Li độ của vật là x = 0. Tần số góc của dao động là: [TEX]\omega = \sqrt{\frac{k}{M+m}}[/TEX]. Biên độ dao động là A = 5cm
+ "Lúc nào đó" mà xe trượt chính là lúc mà lực đàn hồi tác dụng lên xe bằng lực ma sát nghỉ cực đại. Li độ của vật lúc này là x0. Ta có:
[TEX]kx_0 = \mu mg \rightarrow x_0 = \frac{1}{120} (m)[/TEX]
Vận tốc xe lúc này là v0. Áp dụng định luật bảo toàn năng lượng để tìm v0:
[TEX]\frac{1}{2}(M+m)v^2 = \frac{1}{2}(M+m)v_0^2 + \frac{1}{2}kx_0^2 \rightarrow v_0[/TEX]
+ Lúc này hệ dao động chỉ còn xe, tần số góc của dao động là: [TEX]\omega_0 = \sqrt{\frac{k}{M}}[/TEX]
+ Áp dụng định luật bảo toàn năng lượng để tìm ra độ nén cực đại của lò xo:
[TEX]\frac{1}{2}Mv_0^2 + \frac{1}{2}kx_0^2 = \frac{1}{2}kA_0^2 + \mu mg (A_0 - x_0) \rightarrow A_0 = ?[/TEX]
Thời gian để vật đi từ lúc va chạm với lò xo đến lúc lo xo nén cực đại: [TEX]t = \frac{\pi/2 - \arccos(x_0/A)}{\omega} + \frac{\arccos(2x_0/A_0+x_0)}{\omega_0}[/TEX]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
A. 0,345s
