Tìm m để phương trình :
có 2 nghiệm x1;x2 sao cho biểu thức
đạt GTLN.
Phương trình đã cho có [tex]ac=1.(-6)=-6<0[/tex] nên có 2 nghiệm trái dấu
Theo hệ thức Viète ta có:
[tex]\left\{\begin{matrix} x_1+x_2=1-m\\x_1.x_2=-6 \end{matrix}\right.[/tex]
Xét [tex]Q=(x_1^2-9)(x_2^2-4)=(x_1x_2)^2-4x_1^2-9x_2^2+36=(-6)^2-4x_1^2-9x_2^2+36=72-4x_1^2-9x_2^2[/tex]
Có [tex]Q=72-4x_1^2-9x_2^2=72-12x_1x_2-(4x_1^2-12x_1x_2+9x_2^2)=72-12.(-6)-(2x_1-3x_2)^2=144-(2x_1-3x_2)^2\leq 144[/tex]
Dấu = xảy ra khi $2x_1-3x_2=0 \Leftrightarrow 2x_1=3x_2$(vô lí vi $x_1;x_2$ trái dấu)
Có [tex]Q=72-4x_1^2-9x_2^2=72+12x_1x_2-(4x_1^2+12x_1x_2+9x_2^2)=72+12.(-6)-(2x_1+3x_2)^2=0-(2x_1+3x_2)^2\leq 0[/tex]
Dấu =xảy ra khi [tex]\left\{\begin{matrix} 2x_1+3x_2=0\\ x_1+x_2=1-m \\ x_1.x_2=-6 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_1=\frac{-3}{2}x_2\\ \frac{-3}{2}x_2+x_2=1-m \\ x_1.x_2=-6 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_1=-3m+3\\ x_2=2m-2 \\ (-3m+3)(2m-2)=-6 \end{matrix}\right.\Leftrightarrow m=0-or-m=2[/tex]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 có 2 nghiệm x1;x2 sao cho biểu thức
có 2 nghiệm x1;x2 sao cho biểu thức
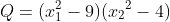 đạt GTLN.
đạt GTLN.
