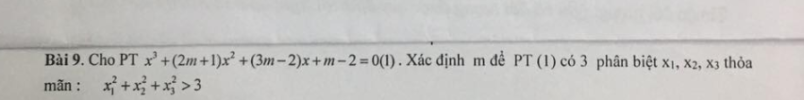Cho phương trình: [imath]x^3 + (2m+1)x^2 + (3m-2)x + m-2 = 0[/imath] (1). Xác định [imath]m[/imath] để pt (1) có 3 nghiệm phân biệt [imath]x_1; x_2;x_3[/imath] thỏa mãn: [imath]x_1^2 + x_2^2 + x_3^2 > 3[/imath]
Mọi người giải giúp em bài này với ạ.
nguyet285@
[imath]x^3 + x^2 + 2mx^2 + 2mx + mx + m - 2x - 2 = 0[/imath]
[imath]\iff x^2(x + 1) + 2mx(x+1) + m(x+1) - 2(x+1) = 0[/imath]
[imath]\iff (x+1)(x^2 + 2mx + m - 2) = 0[/imath]
[imath]\iff \left[\begin{array}{l} x = -1 \\ x^2 + 2mx + m -2 = 0 \end{array}\right.[/imath]
Ta có: [imath]x_1^2 + x_2^2 + x_3^2 > 3 \iff x_1^2 + x_2^2 > 2[/imath] ( với [imath]x_1 ; x_2[/imath] là 2 nghiệm của phương trình: [imath]x^2 + 2mx + m -2 = 0[/imath])
[imath]\iff (x_1 + x_2)^2 - 2x_1x_2 > 2 \iff 4m^2 - 2(m-2) > 2 \iff 4m^2 -2m +2 > 0[/imath] (Đúng với mọi [imath]m[/imath])
ĐK pt có 2 nghiệm p/b: [imath]\Delta ' > 0 \iff m^2 - m + 2 > 0[/imath] (Đúng với mọi [imath]m[/imath])
ĐK có 2 nghiệm khác [imath]-1[/imath] thì: [imath]1 - 2m + m -2 \ne 0 \iff m \ne -1[/imath]
Vậy [imath]m \ne -1[/imath]
Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo kiến thức tại
Tổng hợp kiến thức Hình học cơ bản lớp 10 |
Đại số cơ bản lớp 10
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
