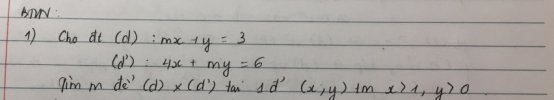Toán 9 Tìm m để d và d’ cắt nhau tại 1 điểm x, y thỏa mãn x>1, y>0

[the_ghost]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho đường thẳng [imath](d): mx + y = 3 , (d'): 4x + my = 6[/imath]. Tìm [imath]m[/imath] để [imath](d)[/imath] cắt [imath](d')[/imath] tại 1 điểm [imath](x;y)[/imath] thoả mãn [imath]x > 1, y> 0[/imath]

 

[Timeless time]

1.
Ta có:
[imath]d: y = 3 - mx[/imath]
[imath]d': my = 6 - 4x[/imath]

TH1: Xét [imath]m = 0[/imath]
[imath]\implies d: y = 3, d': 6-4x = 0[/imath]
[imath]\implies[/imath] Giao điểm của [imath]d[/imath] và [imath]d'[/imath] là : [imath]A\left(\dfrac{3}2 ; 3 \right)[/imath] ( thoả mãn đk bài toán)
TH2: Xét [imath]m \ne 0[/imath]
[imath]\implies d: y = 3 - mx, d': y = \dfrac{6 - 4x}{m}[/imath]
Phương trình hoành độ giao điểm của [imath]d[/imath] và [imath]d'[/imath] là : [imath]3 - mx = \dfrac{6 - 4x}{m} \iff x = \dfrac{6 - 3m}{4 - m^2} \implies y = 3 - \dfrac{m(6 - 3m)}{4-m^2}[/imath]
Theo bài ra ta có [imath]\begin{cases} x > 1\\ y> 0 \end{cases} \iff \begin{cases} \dfrac{6 - 3m}{4 - m^2} > 1 \\ 3 - \dfrac{m(6 - 3m)}{4-m^2} > 0 \end{cases} \implies -2< m< 1[/imath]

Vậy [imath]-2< m < 1[/imath] thì giao điểm của [imath]d[/imath] và [imath]d'[/imath] có [imath]x> 1, y> 0[/imath]

Có gì không hiểu em hỏi lại nhé

Xem thêm: [Ôn thi HKII] Tóm tắt kiến thức toán phần đại số