Để ý: Do phương trình chẵn theo $x$ nên để phương trình có đúng một nghiệm thì nghiệm đó phải là $x = 0$.
ycbt $\iff m = f(x) + \sqrt{x}$ có đúng một nghiệm $x = 0$
$\iff m = f(0)$.
Vấn đề là liệu đây có phải là nghiệm duy nhất không.
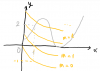
Bạn vẽ thêm đồ thị của $- \sqrt{x}$ lên hình rồi dịch lên từ từ.
- $m \leqslant 0$ thì rõ ràng là $m - \sqrt{x} \leqslant 0$, với dấu bằng tại $x = 0$. Không có nghiệm.
- $m = 1$ thì sẽ có một nghiệm trong khoảng $(0, 1)$. Với $x > 1$ thì $m - \sqrt{x} < 0$ nên không có nghiệm trong khoảng này.
- Tương tự, với $0 < m = f(0) < 1$ thì phương trình chỉ có đúng một nghiệm $x = 0$.
Vậy $m = f(0)$ thỏa đề.
Nếu bạn có thắc mắc gì, có thể hỏi bên dưới. Chúc bạn học tốt!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
