- 29 Tháng mười hai 2020
- 202
- 133
- 61
- 20
- Bình Dương
- Thpt dien hong
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
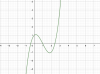
Tập hợp tất cả các giá trị thực của $m$ để phương trình $8^x-3m4^x+3(m^2-1)2^x+3m-29=0$ có ba nghiệm phân biệt là khoảng $(a;b)$. Giá trị của $a+3b$


Cho em hỏi điều kiện y(0) < 0 thì có cần phải thêm vào ko ạ ? vì em thấy ycd.yct <0 và x cđ > 0 thì là đủ rồi chứ nhỉ.

Cho em hỏi điều kiện y(0) < 0 thì có cần phải thêm vào ko ạ ? vì em thấy ycd.yct <0 và x cđ > 0 thì là đủ rồi chứ nhỉ.
Last edited by a moderator: