Toán 9 Tìm giá trị lớn nhất của A

[Nguyễn Ngọc Hạ Đan]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

bài 9 d nha mọi người, em rút gọn rồi chỉ còn x, em hết biết làm tiếp rồi,
Giúp em nha

 

[nhatminh1472005]

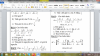
Thứ nhất là rút gọn còn A = [tex]- x + \sqrt{x}[/tex] bạn nhé.
Thứ 2 là câu d làm như sau:
[tex]A = -x + \sqrt{x} = -(\sqrt{x})^2 + \sqrt{x} = -[(\sqrt{x})^2 - \sqrt{x}] = -[(\sqrt{x})^2 - \sqrt{x} + \frac{1}{4}] + \frac{1}{4} = -(\sqrt{x} - \frac{1}{2})^2 + \frac{1}{4} \leq \frac{1}{4}[/tex].
Dấu bằng xảy ra khi và chỉ khi [tex]\sqrt{x} - \frac{1}{2} = 0 \Leftrightarrow \sqrt{x} = \frac{1}{2} \Leftrightarrow x = \frac{1}{4}[/tex] (thỏa mãn điều kiện).
Vậy giá trị lớn nhất của A là [tex]\frac{1}{4}[/tex] khi [tex]x = \frac{1}{4}[/tex].