Giúp mình giải chi tiết bài này với ạ. Vì mình hơi chậm nên mong các bạn giải chi tiết giúp
cảm ơn .
View attachment 85512
GIẢI:
Vì trên đoạn AB có 09 điểm cực đại, nên ta có hệ thức: [tex]4\lambda < AB < 5\lambda[/tex]
Vì M dao động cùng pha với hai nguồn nên ta có: [tex]MA=k\lambda; MB=k'\lambda[/tex]
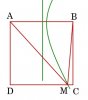
* Theo như hình vẽ, ta có: [tex]2.AB<MA+MB<(\sqrt{2}+1)AB[/tex]
Từ những điều trê, suy ra: [tex]10\lambda<MA+MB<12\lambda[/tex]
Vậy nên, [tex]MA+MB=11\lambda[/tex]
Ta giải hệ: [tex]MA-MB=\lambda(1)[/tex] và [tex]MA+MB=11\lambda(2)[/tex], tính được [tex]MA=6\lambda;MB=5\lambda[/tex]
Vì AB = MC + MD nên xét hai tam giác MAD và tam giác MBC ta lập được hệ thức sau: [tex]AB=\sqrt{(5\lambda)^2-BC^2}+\sqrt{(6\lambda)^2-AD^2}[/tex]
Lưu ý: ABCD là hình vuông nên AB=AD=BC em nha, từ đó đưa về một ẩn suy ra [tex]AB\approx 4,8\lambda[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
