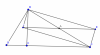
c) Gọi A là giao điểm của MP và IE
PI;PE lần lượt là các tia phân giác trong và phân giác ngoài của [tex]\widehat{P}\Rightarrow PI\perp PE[/tex]
[tex]\Rightarrow \widehat{APE}=90^{\circ}-\frac{\widehat{MPN}}{2}=60^{\circ}[/tex]
Tứ giác MIPE có 3 góc vuông nên là hình chữ nhật
Từ đó chứng minh được [tex]\Delta AEP[/tex] cân tại A
[tex]\Rightarrow \widehat{AEP}=\widehat{APE}=60^{\circ}\Rightarrow \widehat{EIP}=30^{\circ}=\widehat{IPN}[/tex]
mà 2 góc này ở vị trí so le trong
[tex]\Rightarrow IE//NP[/tex]
d) Lấy điểm F bất kì. từ H hạ [tex]KH\perp NP[/tex] tại H
Để [tex]S_{FNP}=S_{MNP}\Leftrightarrow \frac{FH.NP}{2}=\frac{MK.NP}{2}\Leftrightarrow FH=MK[/tex]
[tex]\Leftrightarrow[/tex] Điểm F di chuyển trên 2 đường thẳng song song với NP và cách NP một khoảng bằng MK
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
