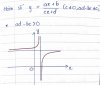
này ko có dấu bằng được nha vì đây là hàm nhất biến
điều kiện để tồn tại hàm nhất biến dạng [TEX]y=\frac{ax+b}{cx+d}[/TEX] là [TEX]ad-bc \neq 0[/TEX] và [TEX]c\neq 0[/TEX]
Tức là [TEX]y’ \neq 0[/TEX]
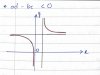
View attachment 184158
View attachment 184159
*hình vẽ này hơi lú hồi đó vẽ nhầm 1 nhánh rùi hic :vv xem để minh hoạ hình dáng đồ thị thôi nha chứ vẽ đúng nó phải như hình trên*
nếu em còn thắc mắc có thể trao đổi thêm nha
Không hẳn là đúng, đây cũng là một thứ dễ bị "gài" trong các đề thi
Khi người ta nhắc đến hàm $y = \dfrac{ax + b}{cx + d}$ thì ngay từ đầu không có điều kiện $ad - bc \ne 0$ đâu. Đó là một trường hợp riêng, và trong một số bài toán mình phải chú ý đến.
Tìm các giá trị của tham số m để hàm số y=[tex]\frac{x-m}{2x-1}[/tex] đồng biến trên từng khoản xác định
Mọi người cho mình hỏi là để hàm số đồng biến trên 1 khoảng thì y' >= 0 với x thuộc khoảng xác định đúng ko. Mà sao mình thấy hầu như các cách giải bài này đều là làm y' > 0 thế. Mong mn giúp đỡ
Trả lời câu hỏi ban đầu của bạn, bạn để ý điều kiện $y' \geqslant 0$ nó còn kèm theo một điều khoản là "$y' = 0$ trên hữu hạn điểm $x$".
... Mình cũng không nhớ câu gốc là gì, nhưng bạn hãy hiểu là: Khi $y' = 0$ tức $ad = bc$, hàm số ban đầu trở thành:
$$
y = \dfrac{ax + \dfrac{ad}{c}}{cx + d} = \dfrac{\dfrac{a}{c} (cx + d)}{cx + d} = \dfrac{a}{c}
$$
Mà đây là hàm hằng luôn rồi nên nó sẽ không đồng biến hay nghịch biến nữa
Những hàm mà phương trình $y' = 0$ không chứa $x$ sẽ bị vấn đề này, bạn có thể suy nghĩ thêm
Mẹo nhỏ là bạn chỉ cần nhớ ngoại lệ duy nhất dạng hàm này thôi: $y = \dfrac{ax + b}{cx + d}$. Mình chưa gặp ngoại lệ nào khác cả.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
