Toán 12 Tiệm cận hàm số

[phuongcandy271101@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Mọi người giúp e câu 42 với ạ!
Em cảm ơn ạ!

 

[Tiến Phùng]

Không có snipping tool thì dùng cái gì ấy cap riêng câu hỏi ra thôi. e chụp cả thế kia nhìn số mũ nhỏ quá không rõ, không thì gõ lại số mũ đi

 

[phuongcandy271101@gmail.com]

Không có snipping tool thì dùng cái gì ấy cap riêng câu hỏi ra thôi. e chụp cả thế kia nhìn số mũ nhỏ quá không rõ, không thì gõ lại số mũ đi

đây ah!

 

[Tiến Phùng]

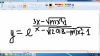
Để có tiệm cận ngang thì khi x->oo thì lim y hữu hạn
ĐKXĐ của căn:
[tex]mx^2+1\geq 0;(2018-m)x^2\geq 0[/tex]
Khi x->oo thì căn tồn tại khi :
[TEX]m\geq 0[/TEX] và [TEX]2018-m\geq 0[/TEX]<=> [TEX]0 \leq m \leq 2018[/TEX]

Điều kiện đủ để có 2 TCN :
nhận thấy khi x-> -oo thì luôn tồn tại lim y hữu hạn => luôn có 1 TCN
Khi x->+oo thì liên hợp:
[tex]y=\frac{(9-m)x^2-1)(x+\sqrt{(2018-m)x^2+1})}{((m-2017)x^2-1)(3x+\sqrt{mx^2+1})}[/tex]
Để lim là hữu hạn thì bậc của mẫu phải bằng bậc tử, vậy
=>[tex]m\neq 2017[/tex]
Kết hợp lại có 2018 giá trị của m