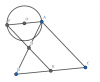
$9.c)$ Gọi $D, E$ lần lượt là trung điểm $AB, BC$, $F$ là điểm đối xứng của $E$ qua $D$.
Có $2\overrightarrow{FD}=\overrightarrow{AC}$ $\Leftrightarrow2\overrightarrow{FD}+\overrightarrow{CA}=\vec0$
Lại có $2MA^2+\overrightarrow{MA}.\overrightarrow{MB}=\overrightarrow{MC}.\overrightarrow{MA}$
$\Leftrightarrow\overrightarrow{MA}.(2\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC})=0$
$\Leftrightarrow\overrightarrow{MA}.(2\overrightarrow{MD}+\overrightarrow{CA})=0$
$\Leftrightarrow\overrightarrow{MA}.(2\overrightarrow{MF}+2\overrightarrow{FD}+\overrightarrow{CA})=0$
$\Leftrightarrow2\overrightarrow{MA}.\overrightarrow{MF}=0$
Suy ra $\left[\begin{matrix}
\overrightarrow{MA}=\vec0\\
\overrightarrow{MF}=\vec0\\
\overrightarrow{MA}\bot\overrightarrow{MF}
\end{matrix}\right.\Leftrightarrow\left[\begin{matrix}
M\equiv A\\
M\equiv F\\
MA\bot MF
\end{matrix}\right.\Leftrightarrow\left[\begin{matrix}
M\equiv A&\\
M\equiv F&\\
M\in (O)&\text{($(O)$ là đường tròn đường kính $AC$)}
\end{matrix}\right.$
Vậy tập hợp các điểm $M$ thoả mãn hệ thức là $(O)$
View attachment 192629
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.