Tích phân hay

G

giotsuong_93

jumongs said:
Tính tích phân [TEX]I=\int_{\frac{\sqrt{3}}{3}}^{1}\frac{\sqrt{(1+x^2)^5}}{x^8}dx[/TEX]
2. Tính diện tích hình phẳng giới hạn bởi: [TEX]y=\left|x \right|+5[/TEX] và [TEX]y=\left|1-x^2 \right|[/TEX]
Bấm để xem đầy đủ nội dung ...


câu1 bạn đặt [TEX]x=tant \Rightarrow dx=\frac{1}{cos^2}dt[/TEX]
đổi cân [TEX]1=tant \Rightarrow t=pi/4[/TEX]
[TEX]\frac{\sqrt{3}}{3}=tant \Rightarrow t=pi/6[/TEX]
thế vào biến đổi ta đc tích phân
[TEX]I=\int_{pi/4}^{pi/6}\frac{cost}{sin^8t}dt[/TEX]
tới đây bạn tự làm hem :D
hình như mình làm bị sai
 
Last edited by a moderator:
L

lantrinh93

jumongs said:
Tính tích phân [TEX]I=\int_{\frac{\sqrt{3}}{3}}^{1}\frac{\sqrt{(1+x^2)^5}}{x^8}dx[/TEX]
2. Tính diện tích hình phẳng giới hạn bởi: [TEX]y=\left|x \right|+5[/TEX] và [TEX]y=\left|1-x^2 \right|[/TEX]
Bấm để xem đầy đủ nội dung ...

:((
bài số 2 chắc có lẽ chia trường hợp giải nhĩ
4 trường hợp :confused:=(( , tớ nghĩ bài tích phân này đơn giản , giải chắc cũng lẹ
 
T

tuyn

mình tìm nguyên hàm,tích phân chỉ việc thế cận là ra:[TEX]I=\int\frac{\sqrt{(1+x^2)^5}}{x^5}\frac{dx}{x^3}=\int\sqrt{\frac{(1+x^2)^5}{x^{10}}}\frac{dx}{x^3}=\frac{-1}{2}\int \sqrt{(1+\frac{1}{x^2})^5}d(\frac{1}{x^2})=\frac{-1}{2} \int (1+\frac{1}{x^2})^{\frac{5}{2}}d(1+\frac{1}{x^2})=\frac{-1}{7}(1+\frac{1}{x^2})^{\frac{7}{2}}+C[/TEX]
 
Last edited by a moderator:
J

jumongs

Tính diện tích hình phẳng giới hạn bởi 2 đường: [TEX]y=\left|x^2-1 \right|,y=\left|x \right|+5[/TEX]. Đáp án mình làm 73/3(dvdt) ai làm kiểm tra hộ mình xíu nha
 
V

vanthanh1501

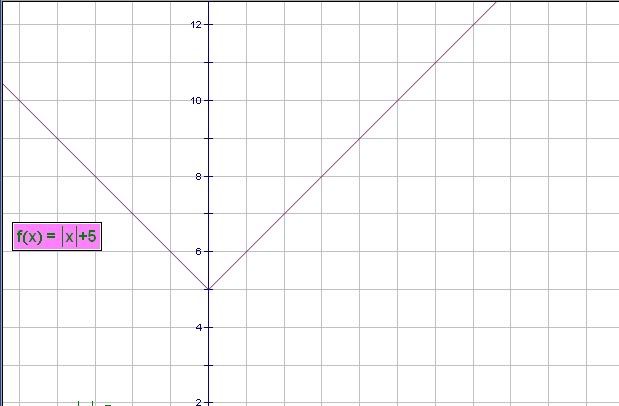
01.jpg



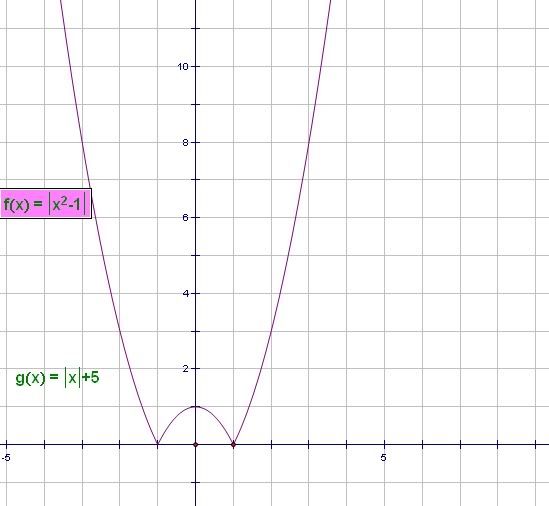
02.jpg


* Với -3\leqx \leq0
[TEX]S_1 = \int_{-2}^{0}|x^2 + x -6|dx = \frac{2}{3}[/TEX]

*Với 0\leqx\leq3
[TEX]S_2 = \int_{0}^{3} |x^2 - x - 6|dx = \frac{9}{2}[/TEX]

--> [TEX]S = S_1 + S_2 = \frac{31}{6}[/TEX]
 
Last edited by a moderator:
V

vanthanh1501

pic này đóng cửa rồi hay sao mà hok ai góp ý dùm hết zạ.
Các bạn xem mình làm zậy có chấp nhận dc ko
 
B

bonoxofut

jumongs said:
Tính diện tích hình phẳng giới hạn bởi 2 đường: [TEX]y=\left|x^2-1 \right|,y=\left|x \right|+5[/TEX]. Đáp án mình làm 73/3(dvdt) ai làm kiểm tra hộ mình xíu nha
Bấm để xem đầy đủ nội dung ...

Kết quả đúng rồi đó bạn. Chúc mừng nhé. :x

vanthanh1501 said:
01.jpg



02.jpg


* Với -3\leqx \leq0
[TEX]S_1 = \int_{-2}^{0}|x^2 + x -6|dx = \frac{2}{3}[/TEX]

*Với 0\leqx\leq3
[TEX]S_2 = \int_{0}^{3} |x^2 - x - 6|dx = \frac{9}{2}[/TEX]

--> [TEX]S = S_1 + S_2 = \frac{31}{6}[/TEX]
Bấm để xem đầy đủ nội dung ...

Bạn MOD của lớp 12 hiện nay đang bận một số chuyện, nên không thể onl đều như trước được. Mong bạn thông cảm cho sự bất tiện này. :) Mình xin thay mặt bạn ấy kiểm tra giùm bạn nhé.

-------------------------

Bạn làm SAI!!! Sai ở chỗ trường hợp -3 <= x <= 0 phải được chia làm 2 trường hợp con là:

  • -3 <= x < -1: Trên đây thì làm số [tex]y = x ^ 2 - 1[/tex] không âm, khi phá trị vẫn giữ nguyên biểu thức.
  • -1 <= x <= 0: Trên khoảng này thì làm số [tex]y = x ^ 2 - 1[/tex] là không dương, khi phá trị phải đổi dấu!!!
Do đó, bạn không thể gộp 2 trường hợp thành 1 như vậy được.

Và tương tự với 0 < x <= 3, bạn cũng chia bị thiếu trường hợp.

Kết luận: Theo đúng quy trình của 1 bài tính diện tích, thì bài này cần chia làm 4 trường hợp nhỏ!!!

-------------------------

Tuy nhiên: Nếu để ý kỹ hơn 1 chút, ta sẽ thấy hàm số [tex]y_1 = |x| + 5[/tex], và [tex]y_2 = |x ^ 2 - 1|[/tex] là 2 hàm số chẵn, tức là có đồ thị đối xứng qua trục tung Oy. Do đó, thay vì chia làm 4 trường hợp, ta chỉ cần chia làm 2 trường hợp là:

  • -3 <= x <= -1
  • -1 <= x <= 0
Sau khi tính tổng 2 tích phân này xong, ta tiến hành nhân 2 là ra kết quả cần tìm. Tiết kiệm được 50% thời gian. B-)

Thân,
 
Last edited by a moderator:
You must log in or register to reply here.
Top Bottom