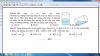
Khi nghiêng, góc tạo bởi mặt nước và đáy là $\alpha$ thì $\tan \alpha = \dfrac{10}{3}$
Đặt gốc tọa độ $O$ vào tâm đáy, trục $Ox$ trùng đường kính đáy (trong đề) hướng ra ngoài màn hình, trục $Oy$ trên đáy hướng về phía nước chạm miệng cốc, trục $Oz$ hướng lên trên
Cắt khối nước cần tính theo một mặt phẳng song song $(Oyz)$ tại vị trí $x$ thì ta được 1 tam giác vuông có các cạnh góc vuông lần lượt là $\sqrt{9 - x^2}$ và $\sqrt{9 - x^2} \cdot \tan \alpha$
Diện tích tam giác này là $\dfrac{5}{3} (9 - x^2)$
Vậy ta chỉ cần tính $$\int_{-3}^3 \dfrac{5}{3} (9 - x^2) dx = 60 \ (\textrm{cm}^3)$$
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.