Câu 18
Ta có [tex]\Delta SAB=\Delta SAC[/tex] (cạnh huyền, cạnh góc vuông)
Kẻ [tex]BI\perp SA\rightarrow CI\perp SA[/tex]
[tex]\widehat{(SAB),(SAC)}=\widehat{IB,IC}[/tex]
[tex]\widehat{BIC}=60^{o}[/tex] hoặc [tex]\widehat{BIC}=120^{o}[/tex]
Xét [tex]\widehat{BIC}=60^{o}\rightarrow \Delta BIC[/tex] đều [tex]\rightarrow BI=a\sqrt{2}[/tex]
Xét [tex]\Delta SAB[/tex] có $BI>AB\rightarrow $ vô lý
[tex]\rightarrow \widehat{BIC}=120^{o}[/tex]
Ta có [tex]V_{S.ABC}=V_{S.IBC}+V_{A.IBC}=\frac{1}{3}.AI. S_{IBC}+\frac{1}{3}.SI.S_{IBC}=\frac{1}{3}.SA.S_{IBC}[/tex]
Đến đây thì đơn giản rồi, em tự tính nhé
Câu 19
Áp dụng công thức [tex]V=\frac{1}{3}B.h[/tex]
Câu 20
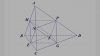
Ta có [tex]V'=V-(V_{A.MNP}-V_{B.MEF}+V_{C.NEG}+V_{D.PFG})=V-4_{A.MNP}=V-4.\left ( \frac{1}{2} \right )^{3}=\frac{1}{2}V[/tex]
[tex]\rightarrow \frac{V'}{V}=\frac{1}{2}[/tex]
Câu 21

Ta có[tex]\frac{d(D,(ABC))}{d(G,(ABC))}=\frac{DH}{GK}=\frac{DI}{GI}=3\rightarrow d(G,(ABC))=\frac{1}{3}d(D,(ABC))[/tex]
[tex]\rightarrow V_{G.ABC}=\frac{1}{3}d(G,(ABC)).S_{ABC}=4[/tex]
Nếu có gì không hiểu thì hỏi lại nhé. Chúc em học tốt

 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.