- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. tính chất
khối chóp [tex]S.A_1A_2..A_n[/tex] có [tex]SA_1=SA_2=SA_3=k[/tex]. khi đó hình chiếu vuông góc của S xuống mặt đáy là H, trùng với tâm đường tròn ngoại tiếp tam giác [tex]A_1A_2A_3[/tex], đồng thời SH cũng là trục ngoại tiếp của tam giác [tex]A_1A_2A_3[/tex].
nếu gọi R là bán kính đường tròn ngoại tiếp tam giác [tex]A_1A_2A_3[/tex] thi đường chao của hình chóp khi đó là: [tex]h=\sqrt{k^2-R^2}[/tex]
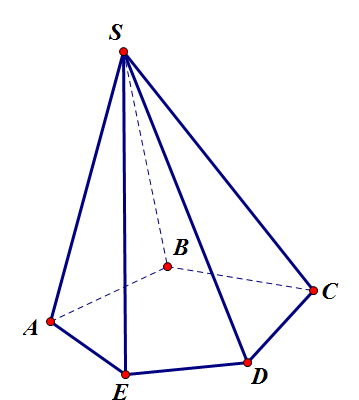
khối chóp [tex]S.A_1A_2..A_n[/tex] có [tex]SA_1=SA_2=...=SA_m=k[/tex], khi đó đa giác [tex]A_1A_2...A_m[/tex] nội tiếp đường tròn tâm H, trùng với hình chiếu vuông góc của đỉnh S xuống mặt phẳng đáy.
2. ví dụ:
ví dụ 1: cho hình chóp S.ABC có đáy là tam giác vuông tại A và [tex]AB=1,AC=2[/tex]. các cạnh bên [tex]SA=SB=SC=\sqrt{3}[/tex]. tính thể tích khối chóp S.ABC
giải:
diện tích đáy: [tex]S=\frac{1}{2}AB.AC=\frac{1}{2}.1.2=1[/tex]
do tam giác đáy là tam giác vuông nên bán kính đường tròn ngoại tiếp: [tex]R=\frac{BC}{2}=\frac{\sqrt{5}}{2}[/tex]
khối chóp có 3 cạnh bên bằng nhau nên chiều cao của khối chóp: [tex]h=\sqrt{SA^2-R^2}=\sqrt{3-\frac{5}{4}}=\frac{\sqrt{7}}{2}[/tex]
từ đó suy ra thể tích là [tex]V=\frac{7}{6}[/tex]
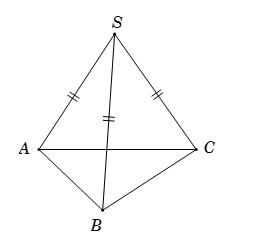
ví dụ 2: cho hình chóp S.ABC có [tex]SA=SB=AB=AC=a[/tex], [tex]SC=\frac{\sqrt{6}}{3}a[/tex]. mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). tính thể tích của khối chóp.
giải:
nếu nhìn trực diện theo hình chóp S.ABC thì không dễ để giải bài toán.
ta xem hình chóp A.SBC có đỉnh là A.
do AS=AB=AC nên hình chiếu vuông góc của A xuống mặt phẳng (SBC) là H, H đồng thời cũng là tâm đường tròn ngoại tiếp tam giác (SBC).
do AB=AC và (SBC) vuông góc (ABC) nên suy ra H là trung điểm cạnh BC.
từ đó suy ra tam giác SBC vuông tại S.
diện tích tam giác đáy: [tex]S=\frac{1}{2}.SB.SC=\frac{\sqrt{6}}{6}.a^2[/tex]
bán kính đường tròn ngoại tiếp tam giác đáy: [tex]R=\frac{BC}{2}=\frac{\sqrt{15}}{6}a[/tex]
chiều cao của khối chóp: [tex]h=\sqrt{SA^2-R^2}=\frac{\sqrt{21}}{6}a[/tex]
suy ra thể tích khối chóp là: [tex]V=\frac{1}{3}.S.h=\frac{\sqrt{14}}{36}a^3[/tex]
khối chóp [tex]S.A_1A_2..A_n[/tex] có [tex]SA_1=SA_2=SA_3=k[/tex]. khi đó hình chiếu vuông góc của S xuống mặt đáy là H, trùng với tâm đường tròn ngoại tiếp tam giác [tex]A_1A_2A_3[/tex], đồng thời SH cũng là trục ngoại tiếp của tam giác [tex]A_1A_2A_3[/tex].
nếu gọi R là bán kính đường tròn ngoại tiếp tam giác [tex]A_1A_2A_3[/tex] thi đường chao của hình chóp khi đó là: [tex]h=\sqrt{k^2-R^2}[/tex]
khối chóp [tex]S.A_1A_2..A_n[/tex] có [tex]SA_1=SA_2=...=SA_m=k[/tex], khi đó đa giác [tex]A_1A_2...A_m[/tex] nội tiếp đường tròn tâm H, trùng với hình chiếu vuông góc của đỉnh S xuống mặt phẳng đáy.
2. ví dụ:
ví dụ 1: cho hình chóp S.ABC có đáy là tam giác vuông tại A và [tex]AB=1,AC=2[/tex]. các cạnh bên [tex]SA=SB=SC=\sqrt{3}[/tex]. tính thể tích khối chóp S.ABC
giải:
diện tích đáy: [tex]S=\frac{1}{2}AB.AC=\frac{1}{2}.1.2=1[/tex]
do tam giác đáy là tam giác vuông nên bán kính đường tròn ngoại tiếp: [tex]R=\frac{BC}{2}=\frac{\sqrt{5}}{2}[/tex]
khối chóp có 3 cạnh bên bằng nhau nên chiều cao của khối chóp: [tex]h=\sqrt{SA^2-R^2}=\sqrt{3-\frac{5}{4}}=\frac{\sqrt{7}}{2}[/tex]
từ đó suy ra thể tích là [tex]V=\frac{7}{6}[/tex]
ví dụ 2: cho hình chóp S.ABC có [tex]SA=SB=AB=AC=a[/tex], [tex]SC=\frac{\sqrt{6}}{3}a[/tex]. mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). tính thể tích của khối chóp.
giải:
nếu nhìn trực diện theo hình chóp S.ABC thì không dễ để giải bài toán.
ta xem hình chóp A.SBC có đỉnh là A.
do AS=AB=AC nên hình chiếu vuông góc của A xuống mặt phẳng (SBC) là H, H đồng thời cũng là tâm đường tròn ngoại tiếp tam giác (SBC).
do AB=AC và (SBC) vuông góc (ABC) nên suy ra H là trung điểm cạnh BC.
từ đó suy ra tam giác SBC vuông tại S.
diện tích tam giác đáy: [tex]S=\frac{1}{2}.SB.SC=\frac{\sqrt{6}}{6}.a^2[/tex]
bán kính đường tròn ngoại tiếp tam giác đáy: [tex]R=\frac{BC}{2}=\frac{\sqrt{15}}{6}a[/tex]
chiều cao của khối chóp: [tex]h=\sqrt{SA^2-R^2}=\frac{\sqrt{21}}{6}a[/tex]
suy ra thể tích khối chóp là: [tex]V=\frac{1}{3}.S.h=\frac{\sqrt{14}}{36}a^3[/tex]
