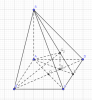
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $G_1,G_2$ lần lựt là trọng tâm của tam giác $ACD$ và $SCD$. Biết rằng thể tích khối chóp $S.ABCD$ là $V$, thể tích khối tứ diện $G_1G_2AB$ là:
Gọi $E$ là trung điểm của $CD$
Ta có: $\dfrac{EG_1}{EA}=\dfrac{EG_2}{ES}=\dfrac{1}{3}$
$\Rightarrow G_1G_2//SA$
Ta có: $S_{ABD}=\dfrac12 S_{ABCD}$
$S_{ABG_1}=\dfrac{BG_1}{BD}.S_{ABD}=\dfrac{2}{3}S_{ABD}=\dfrac13S_{ABCD}$
Suy ra $\dfrac{V_{ABG_1G_2}}{S_{SABCD}}=\dfrac{G_1G_2.S_{ABG_1}}{SAS_{ABCD}}=\dfrac{1}{9}$
$\Rightarrow V_{ABG_1G_2}=\dfrac19V$
Một hình hộp chữ nhật có ba kích thước $\log_2x;\: \log_3x;\: log_4x$ (cm). Gọi $S$ là tổng diện tích các mặt của hình hộp và $V$ là thể tích khối hộp. Biết rằng $S=V$, giá trị của $x$ là:
$S=2\log_2x\log_3x+2\log_4x\log_3x+2\log_2x\log_4x=\log_2x(3\log_3x+\log_2x)$
$V=\log_2x\log_3x\log_4x$
$S=V\Rightarrow \log_2x(3\log_3x+\log_2x)=\log_2x\log_3x\log_4x$
$\Rightarrow 6\log_3x+2\log_2x =\log_3x.\log_2x$
$\Rightarrow 6\log_32.\log_2x+2\log_2x=\log_32.\log^2_2x$
$\Rightarrow 6\log_32+2=\log_32\log_2x$
$\Rightarrow \log_2x=\dfrac{6\log_32+2}{\log_32}$
$\Rightarrow x=2^{\frac{6\log_32+2}{\log_32}}=576$
Có gì khúc mắc em hỏi lại nhé <3
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
