- 8 Tháng năm 2017
- 1,000
- 2,492
- 349
- 28
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài viết thể hiện quan điểm cá nhân của người viết bài.
Thế giới phức tạp này được cấu tạo từ vật chất cơ bản và vận động theo những quy luật. Tương lai chưa đến nhưng có thể được dự báo, quá khứ đã trôi qua nhưng cũng có thể được tìm lại.
Nền khoa học hiện tại có thể giúp con người đến được tương lai, nhưng không thể trở về quá khứ. Ở bài viết này, mình sẽ trình bày góc nhìn của bản thân về thế giới cùng quy luật vận động của nó, theo đó, con người không thể quay lại quá khứ nhưng hoàn toàn tái hiện nó.
I) Cấu trúc của thế giới: Ngắn gọn thôi - vật chất, vận động và các quy luật.
II) Tương lai và quá khứ:
Liệu chúng ta có thể biết được quá khứ và dự đoán được tương lai?
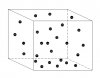
Lấy ví dụ 1 khối không gian trên Trái Đất, trong đó có các viên bi cứng đang chuyển động hỗn độn theo các quy luật vật lý.
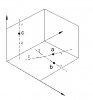
Mỗi viên bi có 1 hướng chuyển động khác nhau, nhưng ta đều biết phương, chiều và vận tốc của chúng. Giờ ta xét 1 mẩu không gian nhỏ trong khối không gian lớn này, gọi đó là vùng A. Trong vùng A đang có 3 viên bi a, b, c chuyển động theo 3 hướng như hình.
Tại thời điểm ta đang xét, 3 viên bi đang ở 3 vị trí a, b, c. Và đang có xu hướng chuyển động như hình vẽ.
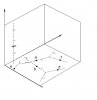
Ta có thể biết được một khoảng thời gian ngắn trước đó, bi a đang ở vị trí a (1), bi b đang ở vị trí b(1) và bi c đang ở vị trí c(1) miễn là chúng ta biết đươc thông số về vận tốc, gia tốc và phương chuyển động của 3 viên bi.
Ta cũng có thể dự báo được sau thời gian t', bi c sẽ đến vị trí c(2), bi a và b sẽ đến các vị trí a(2) và b(2).
Nhưng nếu ta cần biết quá khứ, tương lai của a, b, c ở một khoảng thời gian T, T' lớn hơn thì sao? Ví dụ cách đó 2' và sau đó 2' chẳng hạn. Trước đó 2 phút, a, b, c đã ở ngoài vùng A, vậy ta phải xét trong vùng B lớn hơn.
Trong vùng không gian B rộng lớn hơn, có thêm các bi f, d, e. Để xác định quá khứ của a, b, c vào khoảng 2' trước đó (tại các vị trí -1), trước mắt ta cần xác định được thông số vận tốc, gia tốc, hướng của f, d, e, sau đó ta xét đến va chạm giữa bi a và bi f, giữa bi b và bi d.
Và trong tương lai sau 2', ta tính được vị trí của b sau khi va chạm với e.
Như vậy, ta hoàn toàn xác định được vị trí của bi a, b, c trước 2' và sau 2' thông qua các quy luật. Tuy nhiên số phép tính chúng ta phải thực hiện lúc này là 12 phép, và thông số chúng ta cần là 18 thông số về trạng thái chuyển động của các viên bi.
Tương tự, để biết được quá khứ, tương lai của a, b, c sau khoảng thời gian xa hơn nữa, ta phải mở rộng vùng không gian khảo sát. Khi đó có thể có các bi k, g, h tương tác với hệ các bi này.Để định chính xác vị trí của a ta phải xét va chạm của k với f để f có thể va chạm với a, va chạm của g với d để d có thể va chạm với b.... số phép tính của chúng ta được nhân lên tầm 24 và lượng thông số nhập vào rất lớn.
Thời gian càng dài, số va chạm càng nhiều, số phép tính của chúng ta tăng lên theo cấp lũy thừa. Trên lý thuyết hoàn toàn có thể tính toán được nhưng khối lượng tính quá lớn, và thông số đầu vào cũng quá nhiều, con người không thể kham nổi. Đến đây ta nghĩ ngay đến 1 công cụ là máy tính.
Máy tính có thể lưu trữ rất nhiều thông số, có thể tính toán với khối lượng rất lớn. Chúng ta có thể nhập thông số của tất cả các viên bi trong vùng không gian ban đầu, đưa ra các thuật toán (quy luật va chạm, quy luật hấp dẫn.....) thì máy tính hoàn toàn có thể xác định được vị trí trong tương lai và quá khứ của các viên bi trên.
(Ngắt bài viết tiếp....)
CẤU TRÚC THẾ GIỚI - QUÁ KHỨ VÀ TƯƠNG LAI
Thế giới phức tạp này được cấu tạo từ vật chất cơ bản và vận động theo những quy luật. Tương lai chưa đến nhưng có thể được dự báo, quá khứ đã trôi qua nhưng cũng có thể được tìm lại.
Nền khoa học hiện tại có thể giúp con người đến được tương lai, nhưng không thể trở về quá khứ. Ở bài viết này, mình sẽ trình bày góc nhìn của bản thân về thế giới cùng quy luật vận động của nó, theo đó, con người không thể quay lại quá khứ nhưng hoàn toàn tái hiện nó.
I) Cấu trúc của thế giới: Ngắn gọn thôi - vật chất, vận động và các quy luật.
II) Tương lai và quá khứ:
Liệu chúng ta có thể biết được quá khứ và dự đoán được tương lai?
Lấy ví dụ 1 khối không gian trên Trái Đất, trong đó có các viên bi cứng đang chuyển động hỗn độn theo các quy luật vật lý.
Mỗi viên bi có 1 hướng chuyển động khác nhau, nhưng ta đều biết phương, chiều và vận tốc của chúng. Giờ ta xét 1 mẩu không gian nhỏ trong khối không gian lớn này, gọi đó là vùng A. Trong vùng A đang có 3 viên bi a, b, c chuyển động theo 3 hướng như hình.
Tại thời điểm ta đang xét, 3 viên bi đang ở 3 vị trí a, b, c. Và đang có xu hướng chuyển động như hình vẽ.
Ta có thể biết được một khoảng thời gian ngắn trước đó, bi a đang ở vị trí a (1), bi b đang ở vị trí b(1) và bi c đang ở vị trí c(1) miễn là chúng ta biết đươc thông số về vận tốc, gia tốc và phương chuyển động của 3 viên bi.
Bi a và b đang chuyển động thẳng đều nên trước đó 1 khoảng thời gian t, vị trí của nó sẽ cách vị trí hiện tại một khoảng Sa = va.t , Sb = vb.t theo phương quỹ đạo.
Bi c rơi tự do thì nó sẽ cách vị trí đang xét 1 khoảng Vc.t - g.t^2/2.
Bi c rơi tự do thì nó sẽ cách vị trí đang xét 1 khoảng Vc.t - g.t^2/2.
Ta cũng có thể dự báo được sau thời gian t', bi c sẽ đến vị trí c(2), bi a và b sẽ đến các vị trí a(2) và b(2).
Bi c sẽ cách vị trí hiện tại 1 khoảng S' = Vc.t' + gt'^2/2
Bi a và b va chạm nhau, theo công thức va chạm ta tính được vận tốc và phương chuyển động của chúng sau đó, hoàn toàn có thể suy ra được vị trí của chúng sau khoảng thời gian t'.
Như vậy, bằng các quy luật: chuyển động thẳng đều, định luật hấp dẫn, định luật va chạm, ta có thể dự báo được 1 tương lai gần, cũng như biết được quá khứ gần của 3 viên bi a, b, c thông qua 9 thông số đầu vào và 6 phép tính.Bi a và b va chạm nhau, theo công thức va chạm ta tính được vận tốc và phương chuyển động của chúng sau đó, hoàn toàn có thể suy ra được vị trí của chúng sau khoảng thời gian t'.
Nhưng nếu ta cần biết quá khứ, tương lai của a, b, c ở một khoảng thời gian T, T' lớn hơn thì sao? Ví dụ cách đó 2' và sau đó 2' chẳng hạn. Trước đó 2 phút, a, b, c đã ở ngoài vùng A, vậy ta phải xét trong vùng B lớn hơn.
Trong vùng không gian B rộng lớn hơn, có thêm các bi f, d, e. Để xác định quá khứ của a, b, c vào khoảng 2' trước đó (tại các vị trí -1), trước mắt ta cần xác định được thông số vận tốc, gia tốc, hướng của f, d, e, sau đó ta xét đến va chạm giữa bi a và bi f, giữa bi b và bi d.
Và trong tương lai sau 2', ta tính được vị trí của b sau khi va chạm với e.
Như vậy, ta hoàn toàn xác định được vị trí của bi a, b, c trước 2' và sau 2' thông qua các quy luật. Tuy nhiên số phép tính chúng ta phải thực hiện lúc này là 12 phép, và thông số chúng ta cần là 18 thông số về trạng thái chuyển động của các viên bi.
Tương tự, để biết được quá khứ, tương lai của a, b, c sau khoảng thời gian xa hơn nữa, ta phải mở rộng vùng không gian khảo sát. Khi đó có thể có các bi k, g, h tương tác với hệ các bi này.Để định chính xác vị trí của a ta phải xét va chạm của k với f để f có thể va chạm với a, va chạm của g với d để d có thể va chạm với b.... số phép tính của chúng ta được nhân lên tầm 24 và lượng thông số nhập vào rất lớn.
Thời gian càng dài, số va chạm càng nhiều, số phép tính của chúng ta tăng lên theo cấp lũy thừa. Trên lý thuyết hoàn toàn có thể tính toán được nhưng khối lượng tính quá lớn, và thông số đầu vào cũng quá nhiều, con người không thể kham nổi. Đến đây ta nghĩ ngay đến 1 công cụ là máy tính.
Máy tính có thể lưu trữ rất nhiều thông số, có thể tính toán với khối lượng rất lớn. Chúng ta có thể nhập thông số của tất cả các viên bi trong vùng không gian ban đầu, đưa ra các thuật toán (quy luật va chạm, quy luật hấp dẫn.....) thì máy tính hoàn toàn có thể xác định được vị trí trong tương lai và quá khứ của các viên bi trên.
(Ngắt bài viết tiếp....)
Last edited: