Nếu bạn chỉ cần kết quả thì kết quả tại đây:
https://www.wolframalpha.com/input/?i=515^307+mod+517
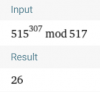
Bạn có thể làm từ từ, hạ số mũ xuống dần nhé: Đầu tiên ta có $515$ khá là gần với $517$ rồi nên
$$
515^{307} \equiv (-2)^{307} \pmod{517}
$$
Tiếp theo, ta có thể bấm phép chia có dư trên máy tính Casio: $\mathtt{2^{30} \div R 517}$ để thu được kết quả $\mathtt{2076870, R = 34}$ tức là
$$
2^{30} \equiv 34 \pmod{517}
$$
Vậy ta có:
$$
(-2)^{307} = -2^7 \cdot 2^{300} \equiv -128 \cdot 34^{10} \pmod{517}
$$
Ở đây $34^{10}$ không chia có dư trực tiêp trên máy tính được, mà ta phải tách ra $(34^5)^2$:
$$
34^{10} = (34^{5})^2 \equiv 430^2 \equiv 331 \pmod{517}
$$
Vậy cuối cùng:
$$
515^{307} \equiv -128 \cdot 331 \equiv -491 \equiv 26 \pmod{517}
$$
Bạn có thể áp dụng từng bước làm này cho hầu như các bài toán tương tự.
- Giảm cơ số về số có trị tuyệt đối nhỏ nhất.
- Tìm số mũ lớn nhất mà máy tính casio còn có thể chia có dư được.
- Lặp lại cho đến khi nào ra thì thôi
Nếu có thắc mắc gì thì bạn có thể hỏi nhé. Chúc bạn học tốt
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
