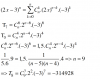1)
View attachment 92139
2)
gọi số cần tìm là abc
=>a+b+c=8
(a,b,c)=(1,2,5),(1,3,4),(1,0,7),(2,0,6),(3,0,5),(8,0,0)
(1,2,5),(1,3,4) : có 3!.2 số
((1,0,7),(2,0,6),(3,0,5) : có 4.3 số
(8,0,0) : có 1 số
=> số các số thỏa đề là : 25 số
3/
a) số có 5 chữ số
số có 5 chữ số khác nhau mà ko có 1 và 5 là : ko có trương hợp thỏa
số có 5 chữ số khác nhau mà chỉ có 1 ko có 5 : có 5!-4!
số có 5 chữ số khác nhau mà chỉ có 5 ko có 1 : có 5!-4!
số số thảo đề là : 6P5-5P4-(5!-4!).2
b) số có 7 chữ số mà chữu số 1 cớ mặt đúng 2 lần là
abcdefg
a=0 => chọn 2 chỗ đặt số 1 vào có 6C2 cách
còn 4 chỗ còn lại xếp 4 số còn lại vào có 4! cách
=> TH này có 4!.6C2 cách
TH bao gồm cả số 0 có : 7C2.5!
=> số các số thỏa đề là : 7C2.5!-4!.6C2
4/[tex]S_{4}=14=\frac{4(U_{1}+U_{4})}{2}[/tex]
ta lại có [tex]U_{5}=U_{1}+4d[/tex]=> [tex]U_{1}+U_{1}+4d=0<=>U_{1}+2d=0[/tex]
ta lai có : [tex]\frac{4(U_{1}+U_{4})}{2}=2(2U_{1}+3d)=14[/tex]
từ đó có hệ rồi => U1 và d => U30 =>S30
5/
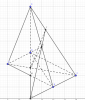
a) bạn nhìn hình làm nha
b) xét 3 mặt phẳng (SAB) ,(SAC) và (FGH)
ta có : (SAB) giao (SAC)=SA
(SAB) giao (FGH)=ME
(SAC) giao (FGH)=GF
mà ME//SA
=> GF//ME//SA
ta có GF//SA mà SA con (SAD)
=> GF // (SAD)
View attachment 92130
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.