Tìm tất cả các giá trị nguyên của tham số m sao cho hàm số y=căn ( -m^2 . x^2 + 2|m|x + 3 xác định trên (1/3 ; 2/3)
YCDB => $\sqrt{m^2.x^2 +2|m|x + 3}$ [tex]\geq[/tex] 0 voi moi x thuoc (1/3;2/3) (*)
TH1
m<0
=> |m| = -m
=> (*) $m^2.x^2 -2mx +3 \geq 0 $ voi x thuoc (1/3; 2/3)
denta'= $4m^2 >0 $ => pt 2 nghiem phan biet
x1 = 1/m <0
x2 = -3/m >0
va $-m^2 <0 $
=>
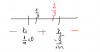
vi the nen => $\frac{2}{3} \leq \frac{-3}{m} $
=>....
TH2 m=0 => (*) 3 >0 voi moi x ( chon)
TH3 m>0
=> (*) $-m^2.x^2 +2mx +3 \geq 0 $ voi x thuoc (1/3;2/3)
=> denta'= $4m^2 >0 $
=> 2 nghiem pb x1 =$\frac{ -1}{m} <0; x2 =\frac{3}{m} >0$, he so a <0
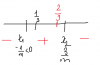
=> $\frac{2}{3} \leq \frac{3}{m}$
=> $m \leq \frac{9}{2}$
=>
Nếu có sai sót, bạn chỉ cho mình nhe


 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.



