VẬT LÍ HMF - SỐ 1
Vật lí quanh ta
Khi vận chuyển đồ vật nặng đi xa, dùng tay xách hay mang vác đều không tiết kiệm sức bằng dùng đòn gánh. Vậy lý do là gì?
Vốn là đòn gánh có tính đàn hồi sau khi hai đầu vật nặng nó nó hơi cong xuống dưới khi người gánh di chuyển về phía trước, thân người lúc nhô cao, lúc thấp xuống còn đòn gánh cũng lúc cong lúc thẳng, nhún nhảy lên xuống. Nếu quan sát kỹ bạn sẽ thấy bước đi của người gánh và chuyển động lên xuống của đòn gánh đều có tiết tấu nhất định. Khi đòn gánh biến thành cong thì vật nặng ở hai đầu trĩu xuống, đòn gánh ép lên vai người gánh khi đòn gánh trở lại thẳng, vật nặng ở hai đầu nhô lên, áp lực của đòn gánh lên vai người hầu như như là biến thành không.
Với người có kỹ thuật tốt hơn người ta điều chỉnh được bước đi của mình sao cho khi đòn gánh nhô lên phía trên thì người gánh cũng vừa bước về phía trước còn khi đòn gánh ép xuống dưới thì hai bàn chân người gánh cũng đồng thời tiếp xúc với đất, khi đó vật nặng không cản trở ở bước đi mà người gánh vẫn có thể đỡ được vật. Điều này giúp người ta cảm thấy đỡ tốn sức rất nhiều.
Thông thường nếu quan sát kỹ bạn sẽ sẽ thấy người gánh thường dùng hai tay kéo vật nặng vào phía trong, đây là một cách làm khôn khéo để đỡ tốn sức vì nếu người gánh không dùng hai tay kéo giữ thì toàn bộ trọng lực của hai vật gánh để lên vai (nơi có diện tích tiếp xúc giữa đòn gánh rất nhỏ) nên phần vai chịu cường độ nén rất lớn lại còn trong một thời gian dài nên sẽ cảm thấy mệt mỏi. Do vậy, để tay kéo giữ vật nặng vào phía trong cánh tay sẽ chịu một phần trọng lực giúp giảm bớt lực ép lên vai.
(Nguồn: Trang 7, Vật Lí - thuộc bộ sách bổ trợ kiến thức chìa khóa vàng, NXB Lao Động.)
Tinh hoa
Phương pháp tìm tọa độ trọng tâm của một vật rắn.
1) Vấn đề
Trong nhiều bài toán của Cơ học Vật rắn, chúng ta đôi khi cần xác định trọng tâm của một vật rắn hoặc một cơ hệ (sau đây mình sẽ gọi chung là cơ hệ luôn). Đối với những cơ hệ đơn giản chúng ta có thể dễ dàng xác định được khối tâm của hệ, ví dụ như một vật rắn hình vuông khối lượng phân bố đều, một vật rắn hình cầu khối lượng phân bố đều... Tuy nhiên, đối với những cơ hệ phức tạp hơn như là vật không đối xứng, khối lượng phân bố không đều...thì sẽ khá khó khăn để ta xác định được khối tâm của hệ. Vì vậy, chúng ta sẽ cùng khảo sát một phương pháp tổng quát để xác định khối tâm của một hệ cơ học nhá!
2) Phương pháp
Ta đặt một hệ trục Oxy vào cơ hệ như hình vẽ. Xét một phần tử có khối lượng $m_i$ của hệ, khối tâm của phần tử này có tọa độ là $x_i, y_i$.
Momen của phần tử này đối với trục quay qua O và vuông góc với mặt phẳng Oxy là: $M_i = m_ig.x_i$
Vậy tổng Momen của tất cả các phần tử thuộc cơ hệ là: $M = \sum{m_i.g.x_i}(1)$
Momen của cơ hệ còn có thể biểu diễn: $M = m.g.x_G(2)$
Từ (1) và (2), sử dụng định lý Va-ri-nhông (Varignon) cho cơ hệ ta có hệ thức: $mg.x_G = \sum{m_ig.x_i}(*)$
Tương tự nếu ta xoay sao cho phương của trọng lực song song với phương của trục Ox, thậm chí là Oz.
3) Kết quả
Dựa vào hệ thức $(*)$ ở trên, tọa độ khối tâm $G$ của cơ hệ khối lượng m biểu diễn như sau:
- $x_G = \frac{1}{m}.\sum{m_i.x_i}$
- $y_G = \frac{1}{m}.\sum{m_i.y_i}$
- $z_G = \frac{1}{m}.\sum{m_i.z_i}$
Trong đó:
- $m_i:$ Khối lượng của một phần tử thuộc cơ hệ
- $x_i,y_i,z_i:$ Tọa độ khối tâm của phần tử khối lượng $m_i$
Ta có thể biểu diễn dưới dạng tích phân:
- $x_G = \frac{1}{m}.\int{x.dm}$
- $y_G = \frac{1}{m}.\int{y.dm}$
- $z_G = \frac{1}{m}.\int{z.dm}$
4) Ứng dụng
Ví dụ 1: Tìm khối tâm của vật rắn có dạng. Biết khối lượng vật phân bố đều
Đầu tiên ta sẽ chia vật rắn thành 3 phần nhỏ có trọng lượng lần lượt là $P_1, P_2,P_3$ như hình:
Sau đó áp dụng công thức tính tọa độ khối tâm:
- $x_G = \frac{1}{m}.(x_1.m_1 + x_2.m_2 + x_3.m_3) = \frac{1}{S}.(x_1.S_1+x_2.S_2+x_3.S_3) = \frac{1}{36}.(0.9+0.24+3,5.3) = $
- $y_G = \frac{1}{m}.(y_1.m_1 + y_2.m_2 + y_3.m_3) = \frac{1}{S}.(y_1.S_1+y_2.S_2+y_3.S_3) = \frac{1}{36}.(5.9+2.24+1,5.3) = $
Ví dụ 2: Một người khối lượng m đang đứng trên một đầu thuyền khối lượng M, chiều dài L. Người đó bắt đầu đi đến đầu bên kia của thuyền. Tìm độ dịch chuyển của thuyền khi người đó đến nơi.
Ta xem người đó như là một chất điểm đang chuyển động và đặt hệ trục tọa độ vào hệ người - thuyền như hình vẽ:
Tọa độ khối tâm của hệ lúc đầu: $x_G = \frac{1}{m+M}.(m.0 + M. \frac{L}{2})$
Tọa độ khối tâm của hệ lúc sau: $x_G' = \frac{1}{m+M}.(m.(L-x) + M.\frac{L-x}{2})$
Tại vì ngoại lực tác dụng nên khối tâm của hệ theo phương Ox không thay đổi nên ta có $x_G' = x_G \Rightarrow \frac{1}{m+M}.(m.0 + M. \frac{L}{2})=\frac{1}{m+M}.(m.(L-x) + M.\frac{L-x}{2}) $
$\Leftrightarrow x = \frac{2m}{M+2m}.L$
5) Thảo luận
Đối với những cơ hệ có hình dạng phức tạp hoặc có khối lượng phân bố không đều thì phương pháp này tương đối hiệu quả, nhưng đối với những cơ hệ đơn giản hơn thì chúng ta có thể mất nhiều thời gian hơn đấy nhé.
Vật lí tranh tài
Vật lí tranh tài là nơi để các bạn yêu thích Vật lí có cơ hội thử thách mình với những câu hỏi Vật lí nâng cao, đồng thời có cơ hội mang về những giải thưởng giá trị cho bản thân mình.
Thể lệ: Mỗi Số "Vật lí HMF", chúng tôi sẽ có 2 - 3 câu hỏi ở phần "Vật lí tranh tài". Chúng tôi sẽ ghi nhận những câu trả lời
đúng và nhanh nhất và sẽ công bố đáp án + tên thành viên giải đúng ở số sau. Câu trả lời được công nhận là
đúng và nhanh nhất là bài trả lời chính xác đầu tiên ở bên dưới bài đăng của số đó. Ngoài ra, nếu như bạn tìm được một cách giải khác đúng mà chưa có ai giải theo cách đó ở trên thì bài giải của bạn cũng sẽ được ghi nhận.
Cách tính điểm: Mỗi một bài viết trả lời
đúng và nhanh nhất thành viên trả lời sẽ nhận được 10 điểm. Sau 8 Số chúng tôi sẽ tổng hợp lại và chọn ra 3 người có điểm cao nhất để trao thưởng. Trường hợp 2 bạn có cùng số điểm thì người có số lượng bài giải nhiều hơn (bao gồm cả những bài không được tính điểm) sẽ được ưu tiên.
Giải thưởng:
- Giải nhất: Huy chương vàng "Trạng nguyên Vật Lí" kèm 10 000 HMCoin.
- Giải nhì: Huy chương bạc "Hội nguyên Khoa Học" kèm 7000 HMCoin.
- Giải ba: Huy chương đồng "Tú tài Khám Phá" kèm 5000 HMCoin.
Câu đố của số này:
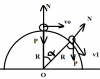
Câu 1: Một vật nhỏ nằm trên đỉnh của bán cầu nhẵn cố định bán kính R, vật được truyền vận tốc đầu $v_0$ theo phương ngang.
a) Xác định $v_0$ để vật không rời bán cầu ngay tại thời điểm ban đầu.
b) Khi $v_0$ thỏa mãn điều kiện trong câu a, xác định vị trí $\alpha$ nơi vật bắt đầu rời khỏi bán cầu.
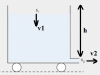
Câu 2: Một bình chứa nước, có một lỗ nhỏ ở sát đáy, có thể chuyển động không ma sát trên mặt phẳng ngang. Diện tích tiết diện của bình là $S_1$, của lỗ là $S_2 << S_1$. Tính gia tốc tức thời của bình khi nó bắt đầu chuyển động.
Thông tin & Liên hệ
Ban biên tập:
Mọi thắc mắc hoặc đóng góp có thể liên hệ:
Hẹn gặp lại các bạn ở số tiếp theo!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Hocmai Forum 
