$\text{ Hình vẽ :}$
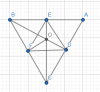
$\\\text{a)}
\\\text{Dễ thấy : }
\\ \widehat{BOC} = \dfrac{1}{2} . \widehat{BAC} + 90^o = 120^o
\\ \Rightarrow \widehat{BOF} = \dfrac{BOC}{2} = \dfrac{120^o}{2} = 60^o
\\ \text{ Ta có }
\\ \widehat{BOE} = \widehat{COD} = 180^o - \widehat{BOC} = 60^o
\\ \text{ Xét } ΔBOE \text{ và } ΔBOF có :
\\ \widehat{BOE} = \widehat{BOF} ( = 60^o )
\\ OB \text{ _ cạnh chung}
\\ \widehat{EBO} = \widehat{FBO}
\\ \Rightarrow ΔBOE = ΔBOF ( \text{ g . c . g} )
\\ \Rightarrow OE = OF ( \text{ Hai cạnh tương ứng })
\\ \text{ Xét } ΔCOD \text{ và} ΔCOF \text{ có : }
\\ \widehat{FOC} = \widehat{COD} ( = 60^o)
\\ OC \text{ _ cạnh chung }
\\ \widehat{ FCO } = \widehat{DCO} ( \text{ Do OC là tia phân giác của góc BCA}
\\ \Rightarrow ΔCOD = ΔCOF (\text{ g . c . g})
\\ \Rightarrow OD = OF ( \text{ Hai cạnh tương ứng})
\\ \text{ Theo trên ta có : }
\\ OE = OF
\\ OD = OF
\\ \Rightarrow OE = OF = OD (\text{đpcm})
\\ \text{b)}
\text{ Xét } ΔOEF \text{ và } ΔODF \text{ có :}
\\ OE = OD
\\ \widehat{EOF} = \widehat{DOF} ( = 120^o)
\\ OF \text{ _ cạnh chung }
\\ \Rightarrow ΔOEF = ΔODF ( \text{ g . c . g} )
\\ \Rightarrow EF = DF
\\ \text{ Ta có : }
\\ \widehat{EOF} + \widehat{EOD} + \widehat{FOD} = 360^o
\\ \Rightarrow 120^o + 120^o + \widehat{EOD} = 360^o
\\ \Rightarrow \widehat{EOD} = 120^o
\\ \text{ Xét } ΔOEF \text{ và} ΔOED \text{ có : }
\\ OE = OD ( cmt )
\\ \widehat{EOF} = \widehat{DOF} ( = 120^o )
\\ OE _ \text{ cạnh chung }
\\ \Rightarrow ΔOEF = ΔOED ( \text{ g . c . g} )
\\ \Rightarrow EF = ED
\\ \text{ Ta có : }
\\ EF = DF
\\ EF = ED
\\ \Rightarrow EF = ED = DF \Rightarrow ΔDEF \text{ là Δ đều }$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
